背理法と対偶命題の証明法は、どのように使い分けるのか

日本で唯一の東大文系に「完全」特化した塾「敬天塾」

東大受験の合否を左右する情報を発信しています！　

背理法と対偶命題の証明法は、使い分けを教えてもらえない。

背理法と対偶命題の証明法の使い分けについてご存知でしょうか？

背理法は簡単に言うと、「命題を否定したものを、真だと仮定して、矛盾を示すもの」です。

背理法の例題としては、√２が無理数であることを証明する問題が非常に有名ですよね。

一方、対偶命題は、条件の「ならば」の前後をひっくり返し、両方とも否定したものです。

教科書にも、問題集にも、必ず例題が載っているのですが、背理法に比べて使用する頻度が少なく、存在感が薄い印象もあるのではないでしょうか？

対偶命題の証明法の代表例は、「ｎの２乗が偶数ならば、ｎも偶数である」などでしょう。

センター試験では毎年のように登場していました。しかし、「対偶を取らせるために用意された問題」も多くて、どのように応用すれば良いかが今一。

背理法と対偶命題の証明法をどう使い分けるか、キチッと明確に教えている先生を、僕はほとんど見た事ありません。
普通の授業では、必ず両方触れますが、教科書でも問題集でも、対偶命題の証明法はあまりクローズアップされず、背理法ばかり使う。
そして、その使い分けに関して触れているのも、非常に少ない。

確かに、背理法を使えば、かなりの問題に対応出来るんですが、ではどう使い分けたら良いのか。

この記事では、しっかりまとめていきたいと思います！

命題には断定型と推論型の二種類がある

まず、命題と条件の話をしっかりしなければなりません。
教科書では、命題をこう定義しています。
命題とは「真か偽かが、はっきりと定まるもの」
ここまでは知ってる方も多いのではないでしょうか。

しかし、命題には二種類あるという事を、皆さんご存知でしょうか。
「ｐである」という形の命題と、「ｐならばｑである」という形の命題です。
区別するために名前を付けましょう。
「ｐである」という形の命題を、断定型。
「ｐならばｑである」という形の命題を、推論型とします。
（この呼び方は、こちらのサイトを参考にしました。）

２種類あると初めて聞いた方、「言われてみれば、確かに！」と納得するでしょう。
これまで見て来た命題も、どちらかに属するはずです。

「否定」をすると、証明が進む（こともある）

では、次に否定の話をしましょう。
命題の証明の仕方にはいくつか方法があります。例えば数Ⅱでは「等式の証明」や「不等式の証明」が登場しますね。（どちらも基本的には、（左辺）－（右辺）をします。）

しかし、このままでは証明できなくなる場合も多数あて、、その時の対処法の一つに「否定する」というものがあります。

何度も例を出しますが、「√２が無理数である」を証明しようとしても、筆が進みません。

そこで、「√２が無理数である」を否定して、「√２が無理数でない」つまり「√２が有理数である」と仮定することによって、筆が進むわけです。

否定をすると良いのはこういう場合

無理数とは「実数のうち有理数でない数」という定義です。
言わば、有理数を拾っていった時の残りカス、みたいに定義されてしまっていて、等式に出来ないのです。
だから、わざわざ否定をして、等式を作って処理します。
※この辺り、証明法の理解が不十分な方は、教科書などを読み直しましょう。

ものすごく単純に言えば、「無理数という言葉に反応して、否定をしろ」ということです。
このように、否定をするために反応すると良いワードがいくつかあります。
「無理数」や「互いに素」、「一つしかない」などなど。

余談ですが、場合の数や確率の余事象の時とあえて混同させると、「少なくとも」とか、「～ない場合」とか、「～以外、以内」などに反応しても良いかもしれません。

背理法と対偶命題の証明法の使い分けは（基本編）

では、やっとですが背理法と対偶命題の証明法の使い分けに行きましょう。

基本的には、
断定型の命題を否定しながら証明する時は、背理法
推論型の命題を否定しながら証明する時は、対偶命題の証明法
と使い分けます。
※対偶命題の証明法は、矢印の前後をひっくり返したい時にも、頻繁に使用します。

「√２は無理数である」は、断定型の命題で、かつ、無理数というキーワードが入っています。
だから、背理法と非常に相性が良い。

「ｎ＾２が３の倍数でないならば、ｎも３の倍数でない」は、推論型の命題ですが、「～ない場合」というキーワードがありますし、矢印の前後をひっくり返した方が証明しやすい。（次数は下げるより、上げる方が楽）
ということで、対偶命題の証明法を使うと良いわけですね。

ここまでが、基本の考えです。

基本が通じない場合が、教科書レベルで出題される

しかしながら、問題があります。
教科書や問題集なんかを覗くとと、推論型なのに背理法を使って証明されている解説が、たくさん見受けられます。

例えば、この問題。
「ａとｂを有理数とする。
ａ＋ｂ√２＝０ならば、ａ＝ｂ＝０であることを証明せよ。」

この問題は、「ならば」があるので、推論型です。

また、√２という無理数が登場しているので、否定をするとよさそう。

すると、基本に則って考えると、対偶命題の証明法を使うはずの問題となります。

しかし、

この問題の解答の一行目は、
「ｂ≠０と仮定する。」
から始まります。つまり、明らかに背理法を使っている！！！

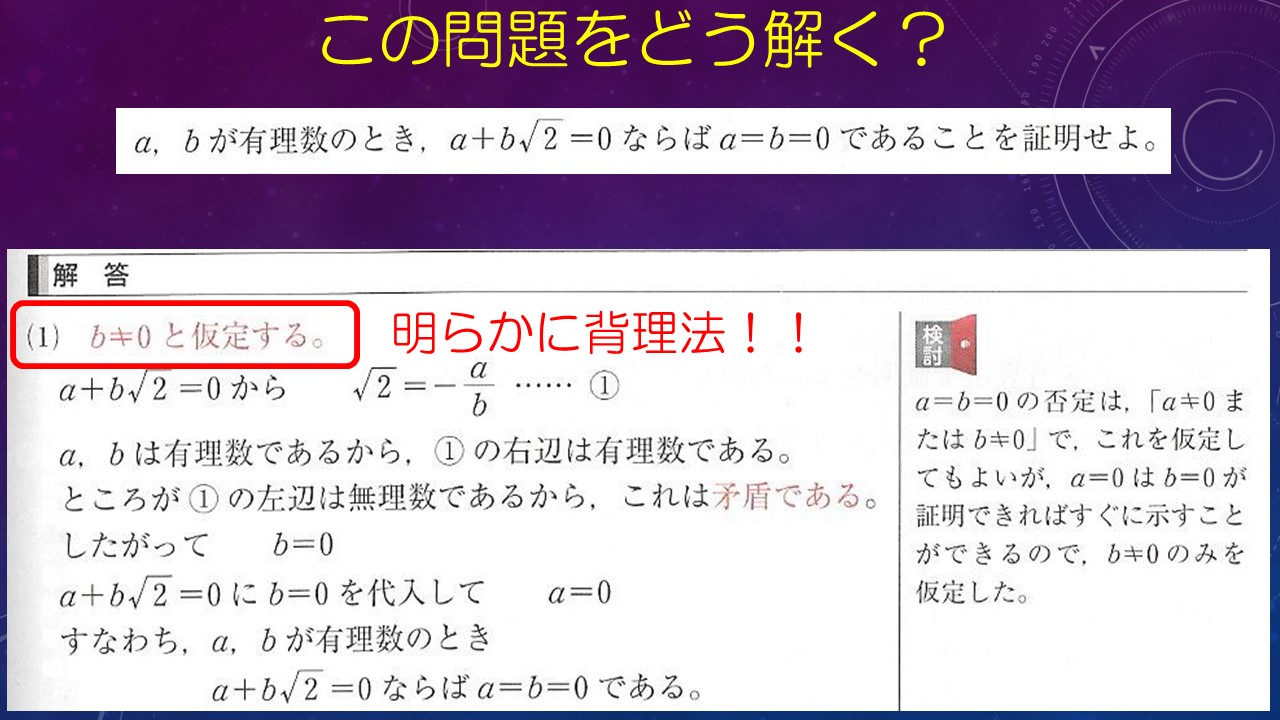
え？？なんで？？
と、困惑するかもしれません。

しかし、大丈夫です。これも解決できます。
ちゃんと、推論型の命題でも、背理法を使う方法があるのです。
それは、どうするのか？

続きはこちらの記事でご覧ください。

東大受験に興味がある方は、敬天塾に関するこちらもご覧ください。
　　↓
◆日本一徹底して東大対策を行う塾　東大合格「敬天塾」

◇プレミアムコース
東大に合格したい新高３生・高卒生を８名限定で募集