【世界一早い東大模試解説】2017秋 河合オープン 文系第1問
2017年秋の河合の東大模試、文系第一問
河合塾の東大模試、文系第一問の解説を始めましょう。
問題の原本が手に入らなかったので手書きですが、一語一句同じに写してあります。
変わった問題ですね。
10進法ではなくて、2進法の問題。
さらに、1が2回だけ登場するという縛り。試験会場の誰もが見た事ない問題でしょう。
もちろん僕も初見です。
但し、問題の誘導のされ方は丁寧。
(1)は10番目の数列を求めよってことですから、1から順に試すがセオリー。
具体的な数字で試すのは、法則を見つけるのに鉄板の方法です。
(2)がa2018の桁数で、(3)がa2018までの3の倍数を数える問題。
直接関係なさそうでも、どこかで使うんだろうなというのを頭に入れながら解きましょう。
「あ~、この問題って誘導だったんだ~」と気付いてはいけません。
数学の問題は全て誘導ですからね。
どういう誘導か気付くためにも、(1)を解き始める前に(2)や(3)まで目を通すようにクセを付けましょう。
(1)規則性を探す
では(1)を解きます。
上に書いた通り、具体的な数字で試すのは、規則性を探るためです。
「解けた!やった~」と言っているようでは不十分。
試験当日では解ける事が大切ですが、自宅で訓練中の時には解けるかどうかよりも規則が探せるかどうかの方が大切です。
今回は、始めから10個を試せという問題ですが、10個試せば規則が見つけられるでしょう、というメッセージと捉えて良いでしょう。
実際やってみると、キレイな規則が見つかります。
↓先ほどと同じ画像。
(2)で桁数に注目しろと言われているので、桁数で区切って見ます。
すると、2桁は1つ、3桁は2つ、4桁は3つ、5桁は4つずつ数列が並ぶのが分かりますね。
また、2進法の1が、右か左にズレていきながら大きくなるのも見て取れます。
この規則が見つかれば、(2)までは解けそうな目途が立ちます。
どんな群数列でも必ず解ける方法
河合の解答解説ではメインの扱いではありませんでしたが、恐らく郡数列だと見て解くのが分かりやすいのではないでしょうか?
先ほど見たように、桁数によって数列の数が増えていきますからね。
数学では特に、自分が得意なフィールドに持ち込むのがコツです。
文章題のままでは解けませんが、数式にした瞬間に手が進む。
無理数のままでは話しが進みませんが、背理法で有理数にした瞬間に筆が進む。
などなど、自分が解ける方法に持ち込めば解けるようになります。
ということで、まずは郡数列の解法を復習しましょう。
郡数列は、ほとんど全員が嫌い。
計算が面倒だし、ややこしいし、あまり面白くない。嫌われてますねー。
私もあまり好きではないのですが、解くのは非常に得意。実は、全く同じ解法で、どんな郡数列でも対応できるってご存知でしょうか?
私は郡数列をこう教えています。
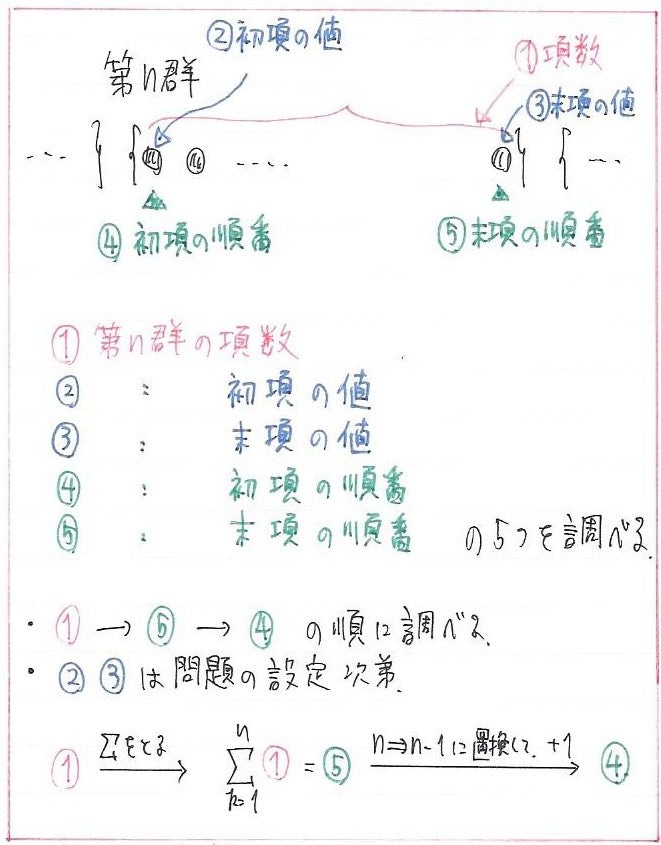
第n群の様子を調べるのは普通。
その中でも、5つ調べるのがオススメ。
①第n群の項数
②第n群の初項の値
③第n群の末項の値
④第n群の初項の順番
⑤第n群の末項の順番
今回のブログの記事は、全て①~⑤の分類と、色分けも統一して手書きの解答を作っているのでご参考に。
図を見れば解き方が分かるかもしれませんが、簡単に書いておきます。
まずは①第n群の項数を調べて下さい。
僕の経験上、第n群の項数を調べるのが難しい問題は、かなり希です。ほとんど見た事がありません。
次に、①の和を取って下さい。(1からnまで)
すると、第n群の末項が、左から数えて何番目かが分かります。つまり⑤第n群の末項の順番です。
これは、必ず成り立ちます。
これで「え~っと、末項に注目すると、階差数列になってるから・・・」などと、余計なことを考える必要もない。
機械的に郡数列がテキパキ解けるようになりますね。
さらに、次は④第n群の初項の順番を調べましょう。
これは、第n-1群の末項の次と考えましょう。つまり、⑤のnをn-1に変えて、最後に+1をすれば良いですね。
ちなみに②と③は問題の設定によってどうにでも変わってしまうので、その場に応じてアドリブをするしかありません。
が、④と⑤を調べることでほとんど決着がつく問題が多いので、やはり困る事はかなり少なくできます。
(2)を群数列で解こう
ここまで調べたら、もう(2)も解けたも同然。
④<2018<⑤を満たすnを調べれば良いのですが、厳密に不等式を解かなくてもOK。
およその数でnを調べて下さい。
では、手書きの解答です。
(3)合同式を使って、設定をシンプルにしよう
では最後。(3)です。
まず注目するのは、問題文に登場する「3の倍数」という日本語。
3の倍数と言われたら、考える事は3つです。
・n=3k、3k+1、3k+2と場合分けをする。(剰余類)
・合同式
・二項定理
この中で、最も使いやすいのは合同式。
これも苦手にする人が多いのですが、使いこなせると非常に便利。
そういえば、夏の駿台の東大模試でも登場しましたね。
リンクを貼っておくので、良かったらご覧ください。
2は3で割った余りが-1。
ということは、-1のn乗が登場するので、偶奇に分ける問題だと分かります。
ただ、今回簡単なのは64群まで調べればよいのが楽ですね。
具体的に書き出しても、あまり大変ではありません。
また、a2018があるのは第64群。
ということは、第63群までは規則的に調べて、第64群だけは一つずつ調べます。
あとは、下の手書きの解答をご覧ください。理解出来ると思います。
細かいところを調べると時間がかかりますが、これは点数を取りに行っても良い難易度でしょう。
少なくとも(2)までは取りたい所ですね。
全く知らない問題が出てきても、セオリーに従って解くことが大切です。
・最初に問題文を最後まで読むこと
・(2)で使う事を念頭において、(1)の規則を探す。
・3の倍数ならば、剰余類、合同式、二項定理と武器を整理しておく。
などなど。
分からないなりに、出来る事はたくさんあります。