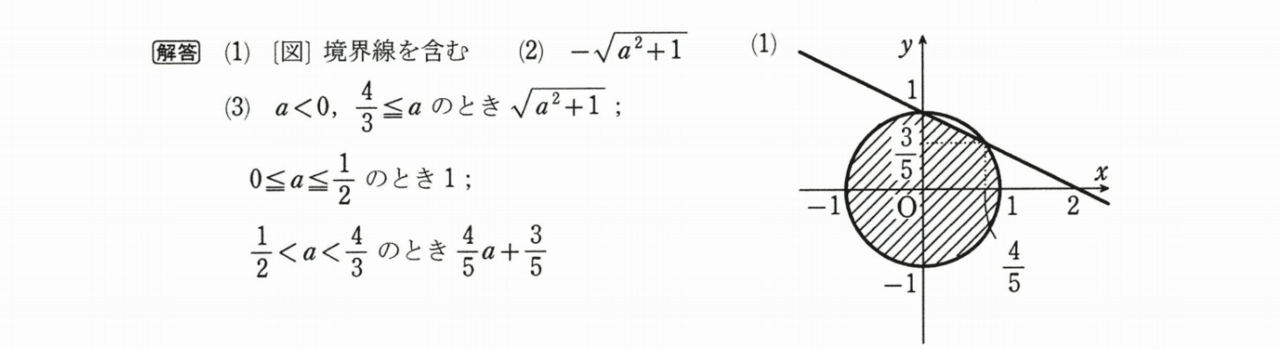数学第7回
こんにちは、スタッフAです!
今回は、コーシーシュワルツと相加相乗平均、線形計画法を扱いました。
最大最小問題では、
まず、グラフがかけるか確認する
グラフが描けないなら、相加相乗平均を検討(分数の最大最小なら相加相乗の可能性が高い)
相加相乗のキーワードは「逆数、分数、最小値(最大値)、和と積」
がポイントだと感じました。それでも解けなければ、線形計画法などの別の解法を検討します。
下記は、相加相乗平均を攻略するために先生が作ったレジュメです。
典型問題が綺麗にまとめられていて「こういう問題が出題されたら、相加相乗平均を使うんだな」とひと目でわかります。

また、今回の授業では、線形計画法を重点的に学習しました。
複数の問題を解けば「=k」とおくというレシピは、多くの生徒が容易にわかると思います。では、そのあとどうするか。
解答が、
・直線の切片
・放物線のy軸方向の移動
・円の半径
などになる場合は、端点か特異点が解になるので、その値を求めることになります。場合分けは、
1 傾きに注目して場合分け
2 kが取る値で場合分け
3 接点の範囲で場合分け
の3つのパターンがありますが、先生のおすすめは1です。
授業中で扱った問題と今回の授業のレジュメを共有しますので、みなさんも解いてみてください。