数学第６回

こんにちは、スタッフAです。
敬天塾の授業の中では、学校の授業で教わらなかった様々なコツや考え方を学ぶことができます。今回の授業で、先生がとくに大事だとおっしゃった、あるいは、ぼくが必ず覚えておかなければいけないと感じたことをまとめました。

・対数の問題では、まず、底の条件と真数>０を書く。
・１微分すると接戦の傾き、２階微分すると変曲点がわかる
・変曲点とは上に凸と下に凸が切り替わるところ（ｙ’’の導関数の符号が変化する点）
・３次関数上と変曲点を通る接線上からは２本の接線が引ける
・「すべての」+等式→恒等式　「すべての」+不等式→最大最小
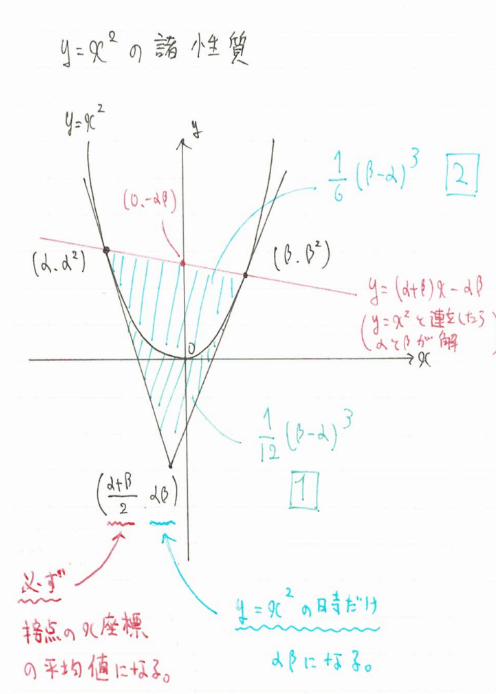
・y=ｘ^２の諸性質（画像を参照）

また、敬天塾の授業で常々言われているのが「別解の検討」です。問題を解き、解説を読み込み、別解を検討してから授業に参加するように指示されています。今回は、下記のような基礎的な問題に対し、どのような解答方法があるか考えました。

与式y=ｘ^２をア、y=ｘ^２+４xをイとします。
① アの接線の方程式とイを連立して、判別式から求める方法
② イの接線の方程式とアを連立して、判別式から求める方法
③ 接線をｙ＝mx+nとおき、アとイ、それぞれと連立して判別式から求める方法
④ アとイそれぞれの頂点における接線の方程式を立て、それらが恒等式になることから求める方法

一つの問題でも様々な解答方法があります。それらをすべて使いこなせるようになることで、どのような問題にも対応できるようになります。与えられた問題を解くだけではなく、常に別解を検討するようにしたいですね。