【世界一早い東大模試解説】2017秋 河合オープン 文系第3問
秋の河合オープン文系第3問
駿台の東大模試も終わりましたね。
皆さん出来はいかがでしたでしょうか?
残っている、河合文系第3問の解説を書いていきましょう。
解く前に情報を読み取れるだけ読み取ろう!
まず問題文を一読して、1文字も解かずに読み取れるものを読み取りしょう。
サイコロを何回も振るということは、反復試行の問題ですね。
また、「初めて、〇〇する確率」ということで、いわゆる優勝決定法の問題です。
反復試行では極めて定番。
例えば、こんなのが例題です。
さらに、(1)から(3)まで、似ている問題が続きます。
(1)は3の倍数、(2)は6の倍数、(3)は12の倍数ということで、徐々に条件が複雑になっているのも、お分かりかと思います。
ということは、明らかな誘導問題。
ま、いつも書いてますが、数学は全ての問題が誘導問題だと思って解いて良いですから、珍しくもなんともないんですけどね。
と何度書いても、誘導だと後で気付いてしまう人が出るので、何度も書いているわけなんですが。
さらに、もう一つ突っ込むと、この問題は積が3の倍数(や6の倍数、12の倍数)になるかどうかが問題になっています。
「積が3の倍数になる」というのは、「少なくとも3の倍数が出るかどうか」を調べる問題ということ。
「少なくとも」は、狭く言うと余事象を使うという目印で、広く言うとベン図を使う目印です。
と、そんな事を考えながら、もう少し丁寧に問題の設定を読み取っていきましょう。
(1)は、教科書例題レベル
(1)から見ていきましょう。
問題の設定としてはサイコロを何度も振って、n回目に初めて3の倍数になる確率です。
ということは、n-1回目までは、一度も3の倍数が出ず、n回目に3か6が出ると言うこと。
これは、カンタン!
教科書の例題レベルですね。優勝決定法の典型問題です。
これは、取らないとダメなレベルでしょう。
優勝決定法はベン図の問題!
では(2)。
今度は、n回目に初めて6の倍数になる確率と言うことなんですが、これは一気に複雑になりました。
というのは、3の倍数に比べて、場合分けが増えるからです。
ポイントは、素数なのか合成数なのかです。
一応説明しておくと、素数というのは1とそれ自身以外に約数を持たない数で、合成数とは素数以外の数です。
3は素数ですから、ベン図を描いた時に(3の倍数)と(3の倍数でない)という領域しか出ません。
しかし、6は6=2×3ですから合成数。
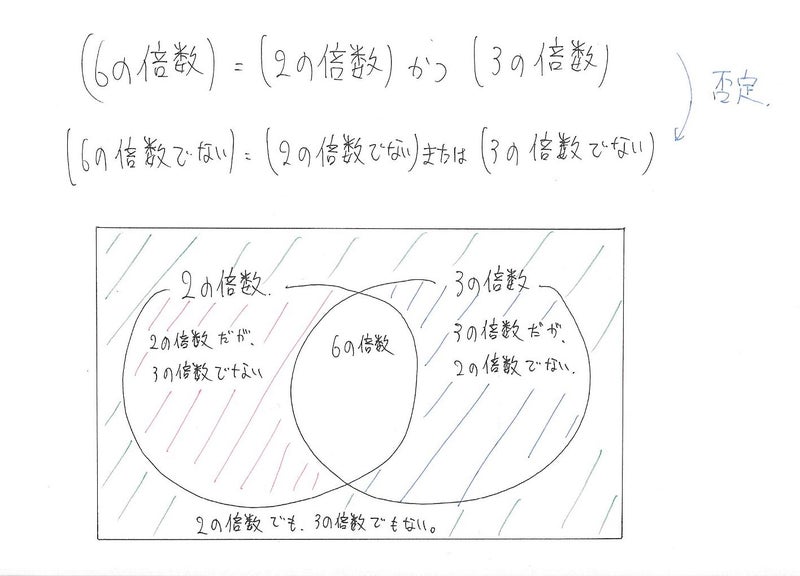
つまり、(6の倍数)=(2の倍数)かつ(3の倍数)となります。
さらに、優勝決定法は、実はベン図の問題と相性が良いです。
n-1回目までと、n回目が否定の関係になります。
今回の問題で言えば、n-1回目までは(6の倍数でない)状態が続きますが、n回目で(6の倍数)になります。
ということは、n-1回目までは
(6の倍数)=(2の倍数)かつ(3の倍数)
を否定して、(ド・モルガンの定理)
(6の倍数でない)=(2の倍数でない)または(3の倍数でない)
として、考えなければなりません。
場合の数・確率の問題では、排反(重複がない)に場合分けをしなければなりませんから、
場合①:2の倍数だが、3の倍数でない
場合②:3の倍数だが、2の倍数ではない
場合③:2の倍数でも3の倍数でもない
の3通りに場合分けをするということです。
反復試行の最大・最小問題
次に、少し脱線して、反復試行の最大・最小問題に少し触れます。
反復試行と言えば、(コンビネーション)×(確率のn乗)×(確率のn乗)の形を想像すると思いますが、最大・最小問題と絡むと、途端に解法が変わります。
教科書的には発展内容の扱いになっていて、模試や入試では難問扱いになることもあるのですが、恐らく皆さん解いた事があるはず。
こういうタイプの問題です。
確率の問題には、くじ引き型とサイコロ型というのがあります。
サイコロ型というのは反復試行や独立試行と呼ばれるもの。
くじ引き型は、試行を行うたびに分母が小さくなってしまうタイプのものです。
比較するために、くじ引き型の画像も貼っておきます。
(順番としては、くじ引き型から見てもらうとわかり易いかもしれません)
というように、くじ引き型とサイコロ型では、最大最小問題の解き方が全く違います。
そして、今回の問題では、要所要所に、サイコロ型の最大最小問題の解法が登場しますので、参考にして下さい。
(3)の場合分けの考え方
では、(3)ですが、求めるのは条件付き確率。
条件付き確率を求める場合は、集合の名前の定義と、確率の定義式を必ず書きましょう。
すると、求める確率は、分母が(n回目で初めて6の倍数になる確率)、分子が(n回目で初めて6の倍数になり、かる、n回目で初めて12の倍数になる確率)となります。
※河合塾の回答では、この辺りが厳密に書いていなかったように思います。
分母は(2)と全く同じなので、そのまま使いまわすとして(笑)
分子はどうかというと、初めて6の倍数になって、しかも12の倍数にもなるということですよね。
ということは、先ほど使った3つ場合分けをもっと細かくすれば良いのです。
先ほどは
場合①:2の倍数だが、3の倍数でない
場合②:3の倍数だが、2の倍数ではない
場合③:2の倍数でも3の倍数でもない
と分けましたが、
場合①:2の倍数だが、3の倍数でない
をもっと細かく分けて、
場合①A:2の素因数が1つだけあり、3の倍数ではない。(2の倍数だけど、4の倍数ではなく、3の倍数ではない)
場合①B:2の素因数が2以上あり、3の倍数ではない。(4の倍数で、3の倍数ではない
とし、
場合②:3の倍数だが、2の倍数ではない
は、そのまま使えます。よって、
場合②:3の倍数だが、2の倍数ではない
と、文字は同じで、色だけ緑に変えておきましょう。
場合③:2の倍数でも3の倍数でもない
に関しては、最後のn回目でどんなサイコロの目が出ても、絶対に12の倍数にならないので、無視することになります。
ということで、上に示した緑色の3つの場合について、それぞれ検討すればOK。
あとは、手書きの解答をご覧くださいませ。
それにしても、計算が面倒ですねぇ。
こんな複雑な計算、当てられる人なんか、ほとんどいないでしょうに。
場合分けも面倒ですし、難しい問題に分類されるでしょう。
(1)は絶対解けなきゃだめだけど、(2)から部分点の問題に変わります。
半分取れたら、中々な問題になるのでは?と予想しますが、いかが?