通過領域をマスターしよう② すだれ法(ファクシミリ論法)と包絡線
【関連ページ】東大文系で頻出の通過領域の解法パターンをすべて紹介した決定版(逆像法・順像法・包絡線・線形計画法など)
すだれ法(ファクシミリ論法)とは?
通過領域の解法の3種類。
・解の配置
・すだれ法(ファクシミリ論法)
・包絡線
のうち、前回は1つ目を書いたので、今回は2つ目と3つ目の解説です。
そうそう、前回書き忘れたんですが、厳密に言うと、これは直線(線分)の通過領域に使われることが多い方法です。
しかし、点の通過領域を求める際には、ベクトルを利用する事も多い。
例えばちょうど去年のの東大文系第2問で使ったものです。(解説記事はこちら)
比較するために、ご覧頂くと良いと思います。
で、すだれ法(ファクシミリ論法)ですが、こんな方法です。
この問題に対して・・・
こう解きます。
xの値で場合を分けて、その時のyの値域を求めます。
xを少しずつ動かして、その時のyを決める。これが、「すだれ」や「ファクシミリ」を想像させるわけですね。
(ちなみに、教学社の東大の文系数学25か年で「すだれ法」と紹介されています。)
包絡線とは?
では、最後に「包絡線」を利用した解法を紹介しましょう。
包絡線とは、「与えられたグラフに、常に接するグラフを求めてしまう」という方法です。
と言われてもよく分からないでしょうから、こちらをご覧ください。
例によって、問題はこちらです。
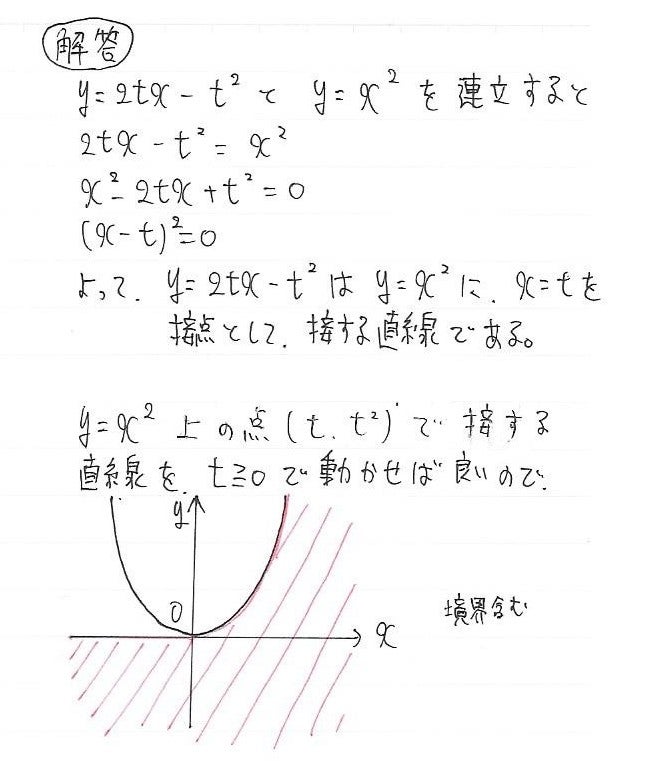
そして、包絡線を使うと、このように解きます。
接線をx>0で動かした時のイメージ図
与えられたパラメータ入りの式を、パラメータで微分します。
次に、元の式と、微分後の式を連立すると、接するグラフが登場してしまうという方法です。
これは、問題によっては、物凄く簡単に解けてしまう解法です。
今回紹介した3つの中でも、最も簡単でしょう。
しかし、包絡線を使いこなせる受験生は、かなり少ない。
まず学校で教わりませんし、教わってもノウハウ化されないままだったり、類題が集めにくかったり。
でも、塾や予備校では積極的に教えるようです。
なんとなく「教えてほしい解法」というより、「教えたい解法」になってる気がしないでもないのですが。
でも、使えたら非常に便利です。
東大では、通過領域の問題は超頻出ですから、必ずマスターしましょう。
【関連ページ】東大文系で頻出の通過領域の解法パターンをすべて紹介した決定版(逆像法・順像法・包絡線・線形計画法など)