ベクトルを学ぶとき、誰もが思う疑問。

「内積ってなに！？」

・ｃｏｓはどこから出てきたの？
・「内積」てことは「外積」もあるの？

色々思うところはあるでしょうが、今回はベクトルの外積について、１本の記事にまとめて書いてみようと思います。

外積は便利！！

ベクトルの外積は、普通は高校で習いません。
しかし、使いこなせると、時々信じられないくらいに楽に問題が解けるため「受験テクニック」として塾や予備校などで教えられる事があります。

では、何が便利かと言うと、
直交するベクトルが簡単に求められる
ことです。

厳密に言うと、空間の中に２本のベクトルがあったとき、両方に直交するベクトルを１本求めることが出来る技術です。

普通に求めると面倒

例えば、こちらの問題をご覧ください。

問、ベクトルｘ（１，２，３）とベクトルｙ（４，５，６）に対して、両方に直交するベクトルを求めなさい。

この問題に対して、普通に解くとこんな感じ。

面白くもない計算がダラダラ続いて、面倒です。

この作業を非常に短縮出来て、なおかつ便利な性質がいくつかくっ付いてくるのが、ベクトルの外積にメリットです。

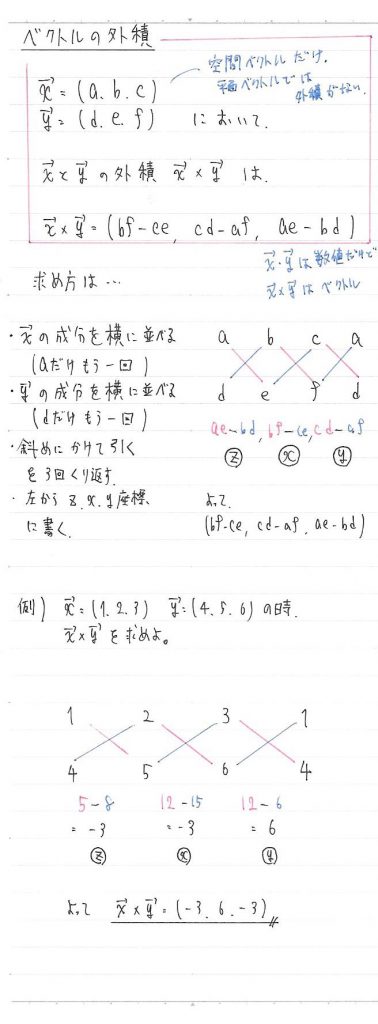
外積の定義

ベクトルの外積の定義は少し複雑。
２本のベクトルの成分を何回か足したり、引いたり、かけたりして求めます。
しかし、一見複雑そうな計算に見えて、実は覚えると大したことがありません。
普通の数字を用いたものなら、ものの１０～３０秒もあれば求められるようになるでしょう。

詳しい求め方はこちらの画像をご覧ください。

外積の性質

次に性質ですが、３つご紹介しましょう。

まず１つ目は、先ほども書いたとおり、元々の２本のベクトルに直交するというものです。
内積を計算してみれば確認できます。

２つ目は、その向きです。
理科を勉強していると「右ねじの法則」や「フレミング左手の法則」が登場しますが、その正体が「ベクトルの外積」だったと確認できます。

ｘからｙに向けて、右手を握ろうとした時に、親指が立っている向きが外積です。

そして最後に３つ目は、大きさです。
これが面白い結果になります。
なんと、元々の２本のベクトルが作る平行四辺形の面積になるのです！！

外積を使った入試問題の例

では、これを使うとどのように便利なのか。
実際の入試問題でも確認できます。

例えばこの問題。

東京大学２０１４年　理系第１問

図を見れば分かりますが、空間内に２本のベクトルで作られる平行四辺形がマンマあります。
この問題の解説は、下のリンク先にありますので、どうぞ参考にご覧くださいね。
２０１４年　東大数学　理系第１問の解説（三角関数・ベクトル・外積・解と係数の関係）

ベクトルの外積は、非常に便利なツールなので、ぜひ使いこなせるようにして下さいね。