数学5月③相加相乗

今回は、関数④相加相乗の応用です。

学んだことを整理しています。

図形の問題では、辺の長さや角度を文字で置いて定義した方が良い。

x＾2＝tと置くのは置換なので、定義域が変わる。注意しよう。

相似条件3つの中では、2角相等が最も頻出。相似になりやすい形は覚えておく。

円と直線の基本的な解法の分岐

円と直線には３つの位置関係がある。

・2点で交わる

・接する

・離れている

上記3つは

・連立して判別式D

または

・円の中心から直線までの距離dと半径rとの距離

から求める。

接する場合は、接線の公式やOP⊥Lでも求められるが、接点や交点を求める場合は前者が有利。

⑸

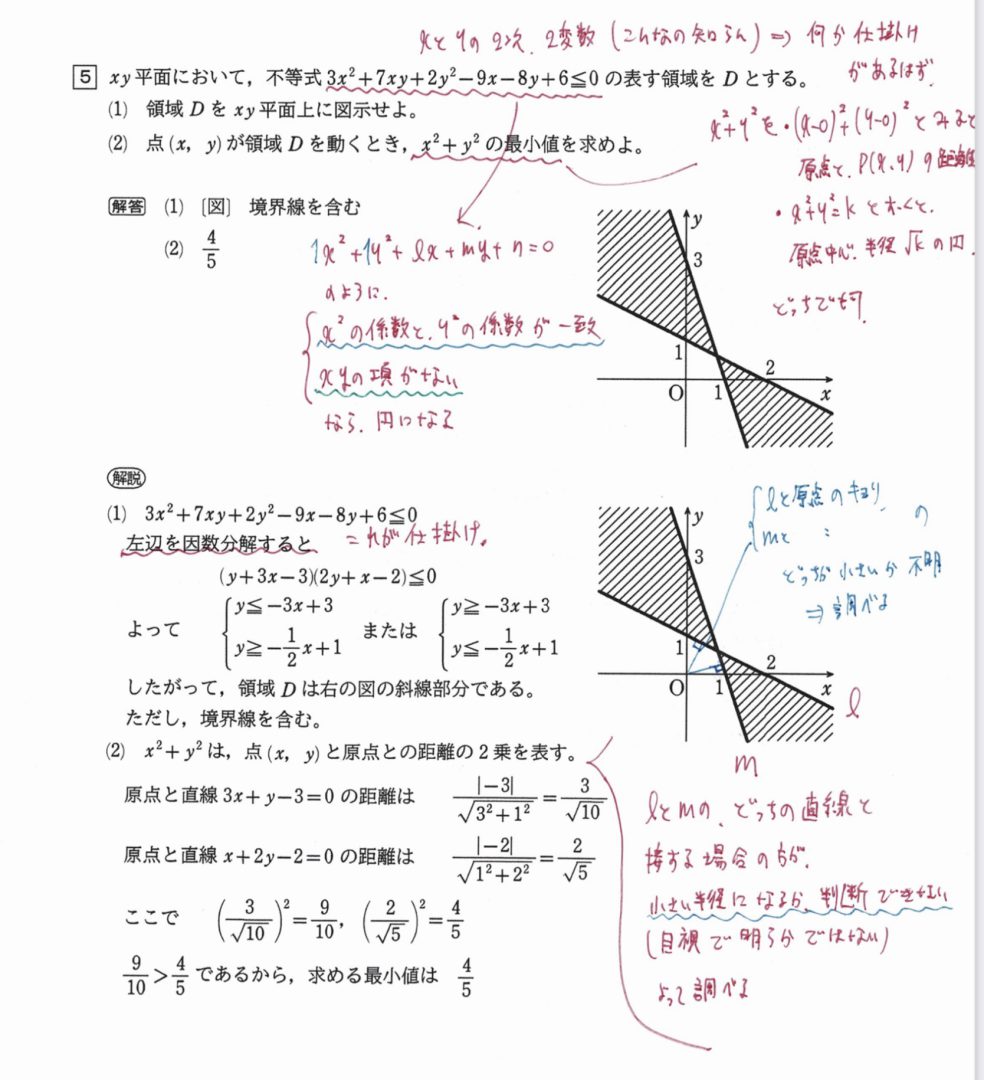
既存の方法では、領域を図示できない問題。

x＾2とy＾2の係数が同じで、xyの項がない場合に円になるが、今回はならない。

だから、因数分解する。

線形計画法では明らかに目視で判断できる場合があり、それは調べずに判断して良い。微妙な場合は、調べないと減点される可能性がある。

放物線と円の位置関係は複雑。

そのため放物線の軸が円の中心を通る問題しか出ない。

3次関数と円はもっと難しい。だから、今年の東大入試で出題された問題も難しい。

連立して、6次方程式をtで3次方程式にして解く問題だった。

（10）

端点と特異点での傾きを出して、場合分けする問題。場合分けが必要な場合は、傾きで場合分けすると良い。

最小値は目視で簡単に分かるが、最大値は目視で判断できない。

円と直線はややこしい。必ず、予習復習を。

次回は、解の配置です。