実数条件について、これでもかと噛み砕いて説明しました。
 平井基之(敬天塾塾長)
平井基之(敬天塾塾長)東京大学理一・文三合格。大手予備校で東大受験専門コースを担当し、集団・個別指導の豊富な現場経験を持つ。
著書に『笑う数学』『同ルート4』(KADOKAWA)、『ビジネスで差がつく論理アタマのつくり方』(ダイヤモンド社)など。
▶ プロフィール詳細はこちら
2文字を2文字に対応させるパターンを学ぼう
普通、「置換」と言ったら1文字を1文字に対応するものが多いです。
例えば、「t=x+2とおく」とした場合、tとxの対応関係を定義していますから、1文字を別の1文字に対応させていると言えます。
しかし中には、2文字を2文字に対応させる問題が登場します。
その代表例が、s=x+y t=xy と置換するパターンです。
これは、xyの2文字を、stの2文字に対応させているので、2文字を2文字に対応させていると言えます。
今回は、このように2文字を2文字に対応させる問題を扱っていこうと思います。
範囲設定はどうする?
さて文字を「置換」する時には、範囲設定を同時に行うことが大事です。
例えば、「t=x+2」と置換した場合、「xは全ての実数」に対し「tは全ての実数」に対応しています。
しかし、「t=x^2」と置換した場合、「xは全ての実数」に対し「t≧0」に対応します。このように、置換前と置換後で、取りうる範囲が変化する場合があります。
というか、たまたま一致することもありますが、基本的には変わります。なので必ず毎回調べる必要があります。
では、「s=x+y t=xy」と置換した場合、どうなるでしょうか?
先ほど書いたとおり、これはxyの2文字を、stの2文字に対応させているのですが、
これは言い換えると、xy平面をst平面に対応させていると言えます。
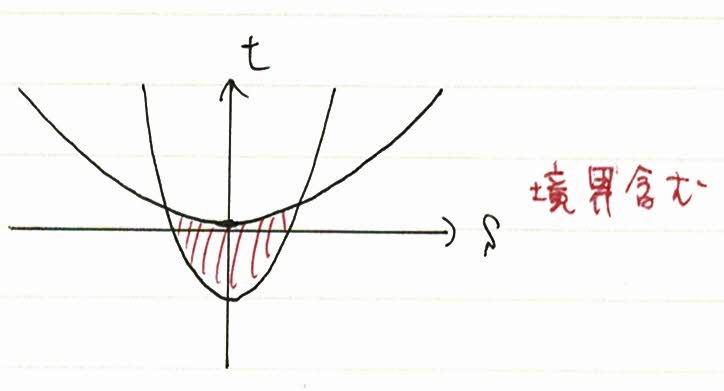
イメージ図はこちらです。
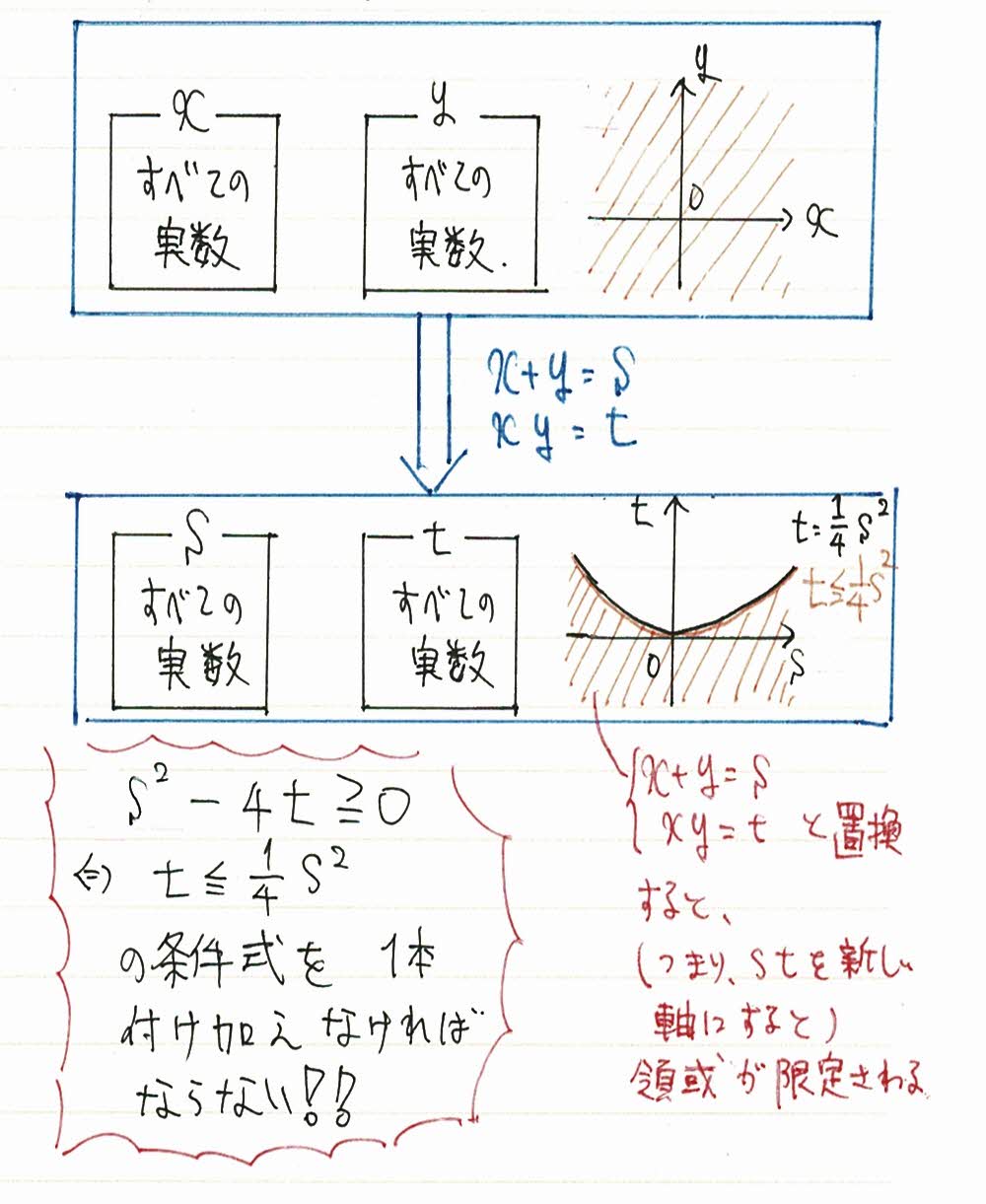
上の図を見ていただくとわかるように、xy平面ではすべての領域で実数xとyが存在できるのですが、
st平面では放物線の下側だけがsとtが存在できる領域になります。
つまり、「s=x+y t=xy」と置換した場合、t≦1/4s^2の式を一本加えるのです。
では、なぜこうなるのでしょうか。
以下に理由を説明していきますが、この理由は多少ややこしい、理解できない人は、とりあえず「s=x+y t=xyと置換した場合、t≦1/4s^2の式を一本加える」という事実を覚えれば、簡単な基本問題を解く分には困らないでしょう。
本質的ではありませんが、受験であればアリかもしれません。
式を加える理由
さて、「xとyは実数全体」と言われると、ものすごく自由に値を取れるというイメージがあると思いますが、実際は制約があります。
それは、虚数ではダメという制約です。
「虚数ではダメ」という制約があるxとyに対し、x+y=s、xy=t という制約がさらに加わるので、もっと自由が利かなくなります。
よって、さきほどみたように放物線の下側の限定されると思ってください。
これを、考えるときに利用するのが、解と係数の関係です。
解と係数の関係を使うと、sとtがある2次方程式の解になっていると考えることができます。
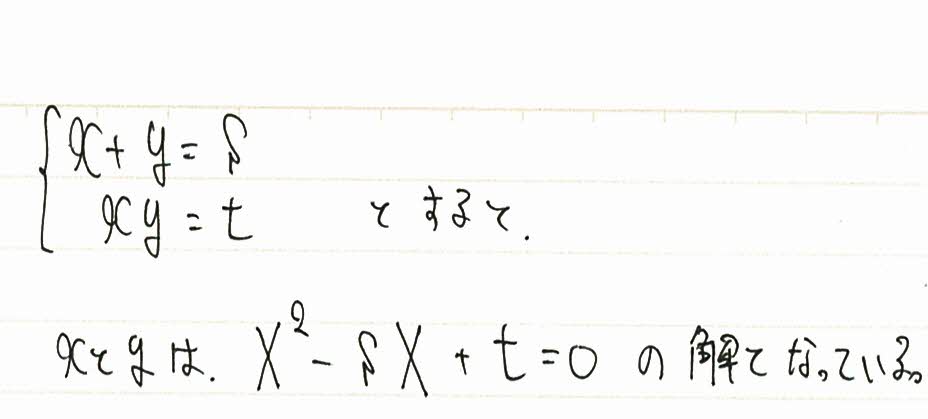
これまで登場していなかった大文字のXが突然登場するので混乱するかもしれませんが、これはどういう意味かというと「sとtは、とにかく何らかの2次方程式の解の和と積になっている」ということです。
何か文字で置かないと困るので、適当にXを使っているだけです。
逆に言えば、sとtは何かの2次方程式の解の和と積になるように、とりうる値を制限されているとも言えます。
もしくは「sとtは、実数を解に持つような2次方程式の係数になっている」という制限があると考えても良いでしょう。いずれにしろ、sとtに制限があることが理解できれば良いと思います。
さて、2次方程式の解になるということは、判別式が0以上になる必要が出てきます。

このように、sとtはこの関係式を満たす必要があるのです。
これを「実数条件」と呼びます。
ここまでをまとめると、
「s=x+y t=xyと置換した場合、実数条件と呼ばれるt≦1/4s^2の式を一本加える」
ということになります。
実数条件を満たさない場合
では、実数条件を満たさない場合はどうなるのでしょうか?
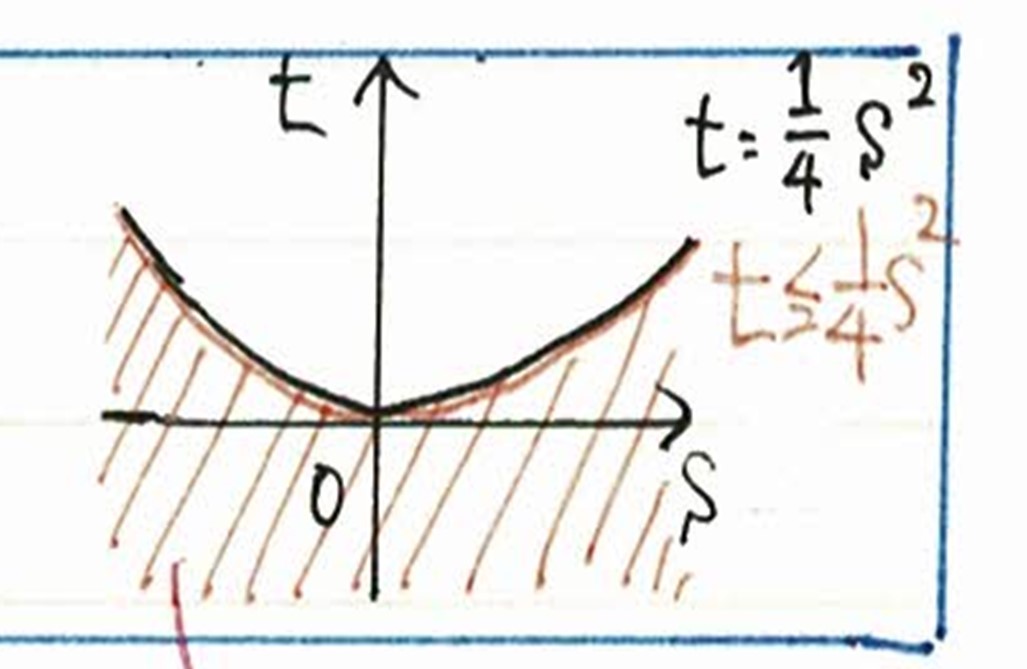
先ほどお見せした、この放物線の領域を満たさないsとtを一つ例として取り上げましょう。
計算しやすそうな例として、s=1、t=1を取り上げました。

x+y=1、xy=1となるxとyを考えてみてください。xとyは実数の範囲では見つからないはずです。
ちなみにこれを解くと、

となり、やはり虚数解になります。
やはり、「xとyが虚数ではダメ」という制約があるからこそ、st平面では放物線の下側でなければならないのです。
例題を解いてみよう
では、実際に例題を解いてみましょう。

※上の例題において、xとyは実数です
この問題の場合の解答は以下のようです。

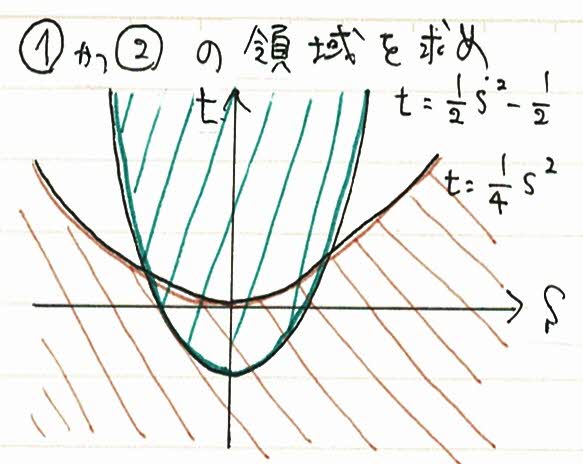
一つの図にまとめると、
↑この図が答えです。
簡単に言うと、実数条件①と、与式の変形をした式②の両方を満たす領域を図示するだけです。
分かってしまえば大したことはないのですが、理屈を理解するのが少々苦労するかもしれませんね。
ぜひ他の問題でも利用して練習をしてみてください。





式を加える理由のところで、s+y=s となっています
ご指摘ありがとうございます。修正しました。
やばい天才すぎる
いつもの置換の時などの、例えがわかりやすくてずっとわからなかったことなのにスッと理解ができました‼︎
おおー、お役に立てたようでとても嬉しいです!
コメントありがとうございます!
分かりやすい!
ありがとうございます。お役に立ててうれしいです。
とてもわかりやすい説明で参考になりました、ありがとうございます!
少し気になった部分があるのでコメントさせていただきます。
> 「sとtは、とにかく何らかの2次方程式の解になっている」
> 逆に言えば、sとtは何かの2次方程式の解になるように…
何らかの二次方程式の解はxとyであり、sとtはその二次方程式の係数を表しているのではないでしょうか?
コメントありがとうございます。
確かにその通りですね。
ただいま、ご指摘頂いた内容に加え
「sとtは、とにかく何らかの2次方程式の解の和と積になっている」
も加えて修正しました。
ご指摘ありがとうございました。
本当に助かりました!!!!!
そうでしたか!お役に立ててないよりです!
とてもわかりやすかったです!
質問なのですが、例題のxとyには実数または座標平面上の点という条件は必要ないのでしょうか。
コメントありがとうございます。
厳密に言うと必要ですし、あった方が親切です。実数条件の内容を説明している文脈の中の例題ということで、ご容赦ください。
ただ、折角ご指摘いただきましたので、記事を修正しました。