教科書や問題集では学べない、背理法の正しい使い方

日本で唯一の東大文系に「完全」特化した塾「敬天塾」

東大受験の合否を左右する情報を発信しています！　

この記事は、前回のこちらの記事「背理法と対偶命題の証明法は、どのように使い分けるのか」の続きです。

まだ御覧になっていない方は、リンク先を読んでから、こちらの記事をご覧ください。

前回の記事の復習

前回は、背理法と対偶命題の証明法の使い分けについて書きました。
命題には２種類あって、それが断定型と推論型。
否定をしたい場合、断定型の証明には背理法を使い、推論型の証明には対偶命題を使うという話でした。

これで完結したら簡単なのですが、そうもいきません。
推論型なのに背理法を使う解法が、教科書や問題集にはよく載っています。
しかもその説明が不十分で、誤魔化さず書かれている参考書に出会ったことがありません。

なぜ、推論型なのに対偶命題ではなくて、背理法を使うのか。
推論型の命題に対して、背理法を使う方法はどういうものなのか。
今日は、この疑問を解消していきましょう。

推論型の命題でも、否定が出来る。

まずは、背理法の時に行う、否定の仕方について話すことからです。
教科書では「条件ｐに対し、ｐでないことを否定という」と書かれています。
当然ですが、この定義ｇは断定型の「ｐである」という命題に対してしか使えません。

しかし、実は推論型の命題にも背理法を使う方法があるのです。
推論型の命題とは「ｐである　ならば　ｑである」という形の命題です。
記号でかくなら「ｐ⇒ｑ」となります。（矢印は“ならば”の意味です）

“ならば”を含む命題に背理法（否定して矛盾を示す）ってどういうこと？？？？
って思うかもしれませんが、背理法の使い方が登場するのです。

今回は難しいことは省いて、使い方だけ簡単にご紹介しますが、
「ｐならばｑ」に背理法を使うと、「ｐ　かつ　ｑでない　となる要素が存在すると仮定し、矛盾を示す」となります。
これさえ覚えていれば、大学受験の背理法の使い方は十分でしょう。

これを理解するには、ベン図を描くと分かりやすいでしょう。

こちらをご覧ください。

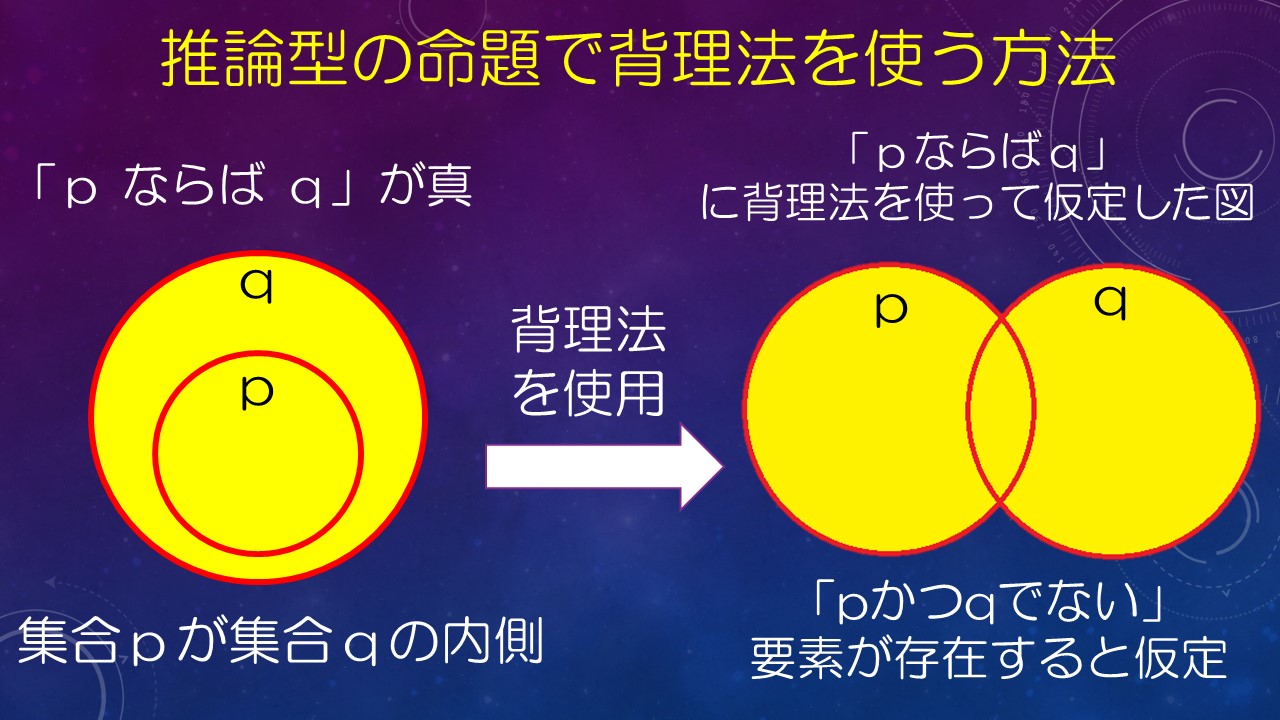
左が推論型の命題が真の状態です。

「ｐならばｑ」が真の場合、ｐが完全にｑの内側にあります。

これに背理法を使うと、どうなるかというと、右側のように

「ｑの外側にもｐの要素が存在する」つまり、「ｐかつｑでない」要素が存在すると仮定するのです。」

つまり推論型の背理法は、
「ｐ　かつ　ｑでない」という要素を仮定して、矛盾を示す技術だとまとめることができます。

例題を使って理解しよう

最後に、前回の記事で紹介した問題の解説をして終わりましょう。

まずは、問題のおさらいから。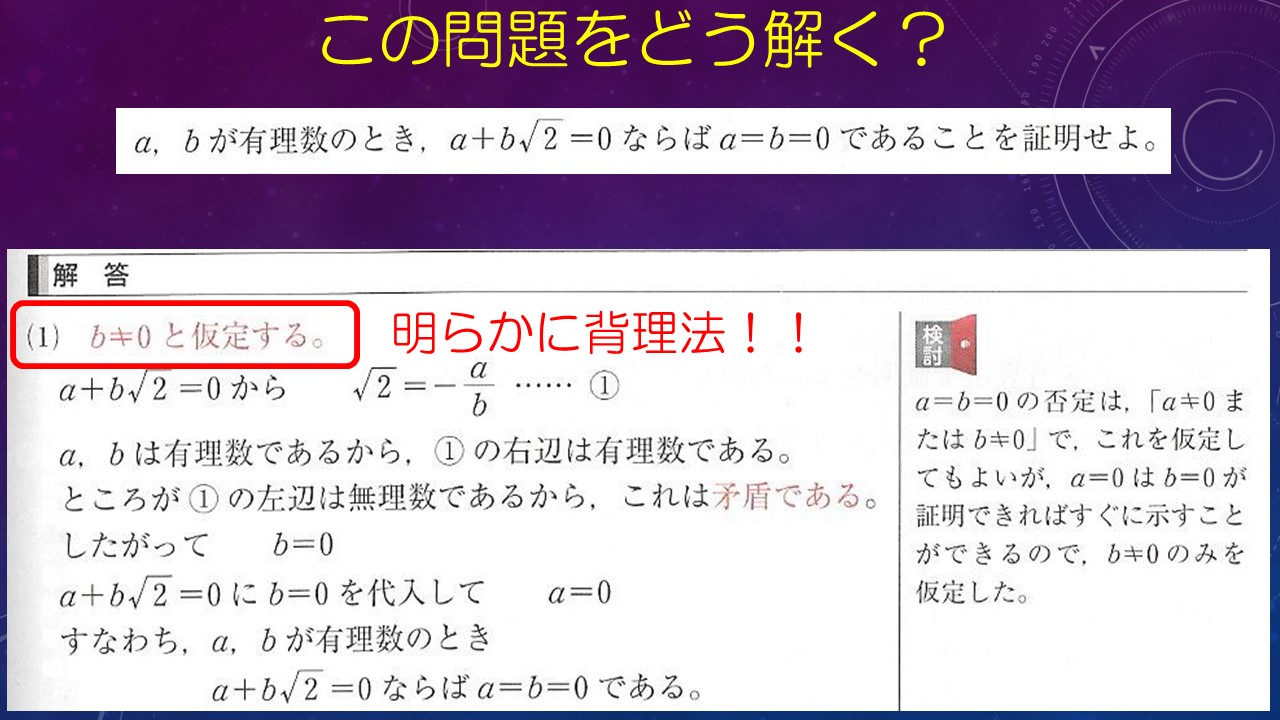

Ｑ「ａとｂを有理数とする。
ａ＋ｂ√２＝０ならば、ａ＝ｂ＝０であることを証明せよ。」

という問題です。（これは、「無理数の相当」の問題です。）

そして、解答の一行目を読むと
「ｂ≠０と仮定する。」
と書かれています。

問題自体は推論型なのですが、背理法を使って証明しています。
ということで、確かに今日の記事のテーマに沿っていますね。

単純に否定しているわけではない

しかしながら、１行目で
「ｂ≠０と仮定する。」
というところが非常に怪しいです。

なぜなら、
元々の命題の示すべき結論が「ａ＝ｂ＝０である」ことですから、これを否定したら
「ａ≠０　または　ｂ≠０」となるはずだからです。

ということで、やはり教科書に載っている方法で書かれている解説ではありません。

では、この１行目は、どのような思考プロセスから書かれているものなのでしょうか？

実は、省略されている論理がある

この問題の解説が厄介なのは、省略されている部分があるからです。この省略部分を知らないと、恐らく絶対に読み解けないのではないでしょうか。

こういうのを知ると、教科書や参考書って、受験生に親切に書かれているわけではないって、つくづく感じますよね。

では、省略部分をおぎなっていきましょう。

問題文では、「ａ＋ｂ√２＝０　ならば　ａ＝０かつｂ＝０」を示せとなっていました。

そして、解説の１行目では「ｂ≠０と仮定する」となっていました。

この間に、

「ａ＋ｂ√２＝０　ならば　ｂ＝０」を示せば、自動的にａ＝０も示せる。よって、

「ａ＋ｂ√２＝０　ならば　ｂ＝０」を示せばよい。

という省略があるのです。

これによって、本来

「ａ＋ｂ√２＝０　ならば　ａ＝０かつｂ＝０」

を示す問題だったのですが、ゴールを単純にして、

「ａ＋ｂ√２＝０　ならば　ｂ＝０」

と言い換えているのです。

これに、さきほど説明した「推論型に背理法を使う方法」を適用すると

「ａ＋ｂ√２＝０　かつ　ｂ≠０　となる要素が存在すると仮定する」という１行目が書けるのです。

よく見ると一応書いてある。

先ほどの画像を見ると、実はしれっと書いてありました。ご覧ください。

書いてあると言えば書いてありますが、こんなの教科書で習う内容ではないですし、なぜ否定するとそのようになるかの理由や証明が書いていません。

余談ですが、参考書もテキトーだなと思いますね。

あは、参考書通りです。

上の画像の通りに証明してもらえれば良いと思います。

まとめ

これで、背理法と対偶命題の使い分けについての疑問が解消されたのではないでしょうか？

まとめると、

この２枚の画像を使えれば十分でしょう。

皆さんの勉強の参考にしてください。

東大受験に興味がある方は、敬天塾に関するこちらもご覧ください。
　　↓
◆日本で唯一の東大文系に「完全」特化した塾「敬天塾」

　◇プレミアムコース
　万全の東大対策をしたい新高３生・高卒生を８名限定で募集！

　◇東大受験生のための図書館「知恵の館（やかた）」
　東大受験の合否を左右する情報を発信しています！

　◇映像授業コース【東大文系数学】
　特定科目の苦手を克服したい方、コストを抑えたい方向けです。

◆敬天塾公式HP
https://exam-strategy.jp/