2024年東大文系数学(第2問)入試問題の解答(答案例)・解説
目次
2024年 東京大学数学 文系第2問

(1)今年一番簡単な問題
今年の問題は、第1問と第3問に(1)からやや解きづらい問題が出題されました。どちらも典型的な解法で通用するのですが、ひねりが加えられています。
ということで、数学がとても苦手な人にとっては、この第2問(1)しか解けなかったという人も多いことでしょう。
解説するまでもないレベル、とも言い切れるような「教科書の例題」ですが、常用対数のlog2が数値ではなく、不等式で与えられていることに、やや戸惑う人もいるでしょう。
理系の受験生や、数学の先生からしてみると、何ともないことかもしれませんが、数学が苦手な方は、こういうちょっとした変化で崩れてしまうものです。
log2が不等式で与えられていようと、やることはほとんど変わりません。最後に、最小のnを特定するところで、計算量がちょっとだけ増えるだけです。以下の解答例を見て「なるほどな」と確認しておいてください!

(2)理系ならすぐわかるけど・・・
さて、(2)に行きましょう。
これまた理系の先生からしてみると「大した事ない問題」と思うかもしれませんが、文系の皆さんはかなり苦労したのではないかと思います。
確かに、考えることや構造は簡単なことです。しかし、文系の受験生は過去に解いたことがあるパターンしか対応できない生徒がおおく、その場で自分で考えて立式するとか、計算するっていうことがなかなかできません。
今回も、わかっちゃえば簡単なのに、自分では発想できないという、絶妙なラインの問題です。
余談ですが、最近の東大では、この絶妙なラインの問題をよく見かけます。
先に答えを予測できちゃう問題
まずは常套手段として、(1)と比較しましょう。
(1)の答えは28でした。では、(2)の答えは、どのくらいの数字になるでしょうか?
この問いに(仮説でも良いので)答えられれば、この問題の本質的なところは理解していると言ってよいでしょう。そう、この問題は答えが先に出てしまう問題なのです。
ズバリ答えは28。(1)と同じです。
ただし、予想や仮説として、27と予想した人も全然OKです。26でも良いですが、26だとちょっと甘いかな。
合格レベルとして許容できるのは27までです。
「発散速度」が分かれば、答えが予測できる。
では、なぜ答えが予測できるか。というか、なぜ(1)と同じになると予測できるのか。
「発散速度」を理解すればわかるでしょう。
発散速度とは、数Ⅲの極限を勉強すると学ぶ概念です。
(だから理系の人にしてみると、当たり前なので、文系の人の何倍も簡単に見える問題なのです。)
細かい定義などは面倒なので、ここでは直感的な理解を重視して説明すると「数字の大きくなりやすさ」のようなものでしょうか。
例を出しましょう。
xに1,2,3・・・・と、段々大きな数字を代入していくとします。
この時、x^2とx^3では、どちらが数字が大きいでしょう。もちろん、x^2より、x^3の方が大きいですね。こんな感じで、別々の関数を比べたときに、数字が最終的に大きくなる関数が「発散速度が大きい関数」で、逆になかなか大きくならない関数が「発散速度が小さい関数」です。
これが理解できれば、発散速度を理解したも同然です。ということで、別に難しいものではありません。
数ⅡBまでに登場する関数で、速度の優劣をつけてみましょう。
もっとも小さいのが、sinxとcosxですね。
xにどんな大きな値を代入しても、ー1と1の間をウロウロして、全然数字が大きくなりません。
まあ、コイツは例外みたいなヤツですね(笑)。普通は、ちゃんと大きくなり続ける関数で比較します。
次がlogxでしょう。(底は1より大きいとしておいてください)
logxのグラフを考えると、確かにグラフはずっと大きくなり続けますが、その速度はメチャクチャ遅いです。例えば、底が2の場合は、xが2倍になって、やっとyが1増えます。
xが10000から20000に増えて、やっとyが1増える。ほぼ真横のグラフですが、ちゃんと増加しているというグラフなんですね。
次が整関数と言われる、x^nの関数です。x^2とかx^3とかですね。
もちろん、nが大きくなれば、発散速度が速くなります。
最強なのが指数関数です。2^xとか3^xとかですね。
こいつ等はメチャクチャ早いです。
y=x^100と、y=2^xを比べてどちらが発散速度が速いと思いますか?
100乗もしていれば、さすがにかなり早いと思うかもしれませんが、違います。xに小さい値を代入すれば、x^100が大きいですが、xに大きい値を代入すればするほど、2^xの方が圧倒的に大きくなります。
大きい値というのは、100や200ではありません。千、万、億、兆、京・・・と続くよりもっと大きな値です。こういう大きな値を代入すると、100乗するより、2倍、2倍と倍にしていった方がはるかに大きくなります。
4^mと5^mも、圧倒的な差がある
もう少し発散速度にお付き合いください。
今回登場しているのは、4^mと5^mです。指数関数の底が1だけ違う関数ですね。
しかし、この2つを比較しても、圧倒的に発散速度が違います。
毎回4倍ずつされる関数と、毎回5倍ずつされる関数ですから、何回も繰り返せばかなりの差になっているというわけです。
余談ですが、こんな数式を見たことがあるでしょうか。
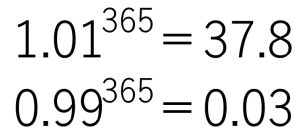
毎日、自分が1%ずつ成長した場合と、毎日1%ずつ退歩した場合、1年後にどれくらいの差がついているか。
という例え話によく使われる式です。
なんと、毎日1%ずつ成長すると、1年後には実力が38倍近くになるけど、1%ずつ退歩するとたった3%になってしまうんですね。
この指数関数は、底が0.01しか違いません。しかし、365乗すると大きな差になります。
話を戻すと、4^mと5^mでは大きな差になるのがお判りでしょうか?今回は高々28乗くらいですが、それでも結構差が付きます。
5^mの方が圧倒的に大きい
ということで、5^mの方が圧倒的に大きく、4^mは圧倒的に小さくなるだろうという予測が出来ました。
発散速度を知っていると、こういう予測が簡単にできてしまうんですね。
5^m+4^m>10^19 の左辺においても、4^mはほとんど大きさに寄与していないということになります。
例えば、100兆+1万みたいな感じだと思ってください。1万の部分はそんなに貢献していないわけです。
ということは、この式は実質的に
5^m>10^19 を考えているのと同じ。つまり、(1)と同じ式を考えているに過ぎないのです。
証明して終わり
では、最後に証明していきましょう。
4^mはほぼ無視できるということで、我々の仮説は、「与式を満たす最小のmは28」です。
ということは、m=27の時に、与式を満たさないことを示せばOK。5^27+4^27を計算して、10^19未満であることを示しましょう。
ここで、5^27や4^27を実際に手計算することもできますが(実際にやった人がいるみたいですね笑)
実際のところは現実的ではないので、セオリー通り対数を取ります。
この時、5^27+4^27全体を対数にとってはダメですよ。別々に対数を取ってください。
![]()
こうやって、別々に対数をとる計算をしたことがない人が多いでしょう。私もしたことがありません。(多分)
ココが難しいところですね。過去に解いたことがあるパターンから逸脱するので、非常に難しく感じるでしょう。(というか、別々に対数をとるという発想すら出てこないかもしれません)
この発想や計算が難しいだろうということで、私はこの問題の難易度判定をやや難にしました。こういう場合はせめて「対数をとって5^27+4^27<10^19を示す」など、方針は書いておきましょうね。
では、手書きの解答をご覧ください。
2024(2)文数 解説オマケ
今回は、発散速度を中心に解説を書きました。
なぜ私がこんなに発散速度に注目して書いたかというと、数Ⅲの内容だからです。
「数Ⅲのことは文系の受験生はわからないでしょ。わかりやすく解説してあげるよ」という優しさもあるにはありますが、そこがメインではありません。
文系受験でも、数Ⅲが分かっていた方が良いという事実を示すためです。
もちろん、数Ⅲ全部を履修した方が良いとは思いませんが、一部の考え方などは文系の皆さんにも必要です。
「東大入試は決められた範囲からしか出ないよ」という嘘に騙されてはいけません。どんな知識が役に立つかわからないのが、東大入試です。
気づいた時や出会った時だけでも良いので、数Ⅲだろうが何だろうが学んでおきましょう。
「自分は文系だから数ⅡBまでで良いんだ」などと閉鎖的に考えてしまう人は、自ら駒場から後ずさりしているのです。
【さらに深く学びたい方のために】
敬天塾では、さらに深く学びたい方、本格的に東大対策をしたい方のために、映像授業や、補足資料などをご購入いただけます。
ご興味頂いたかたは、以下のリンクからどうぞご利用下さい。

解説2024.jpg)



解説2021-300x161.jpg)
