1997年東大文系数学(第1問)入試問題の解答(答案例)・解説(強化帰納法、3項間漸化式、対称式)
1997年 東大数学 文系第1問
さて、数学の解説記事の復活です。整数問題の克服をさせていきましょう。 まずは問題からです。
これまで2回分、東大の整数問題を解説書きましたが、その2問は基本中の基本。 今回の問題からは、東大らしい整数問題を連続して扱います。 ちょっと古いですが、まずはこれをおさえると良いでしょう。 では、解説スタートです。
有名事実の証明問題!
さてこの問題、有名事実の証明をする問題です。
物理なんかでは、公式の証明自体が入試問題になることがありますが(典型的なのは、気体の分子運動論など)数学では、少し珍しいですね。
この問題に関しては、証明の過程まで含めて覚えてしまうのが良いでしょう。
では、具体的に流れを見ていきます。
問題の流れが、強化帰納法になっている。
これはどういう問題かというと、
a^n+b^nに対して、
n=2の時と、n=3の時に4の倍数となれば、あらゆるnで4の倍数となることを証明する問題です。
実は、n=2からスタートではなくて、n=1からスタートしても成立します。
つまり、
「n=1の時と、n=2の時に4の倍数となれば、あらゆるnで4の倍数となる」
というのが有名事実です。
この赤字の部分が有名事実なわけですが、よく読むとまさに「強化帰納法」そのものになっていることがわかりませんでしょうか?
数学的帰納法は、
n=1の時の成立を示すと、あらゆるnに対して成立することを証明する方法ですが、
これの発展版として、強化帰納法があります。
そして、帰納法でも、強化帰納法でも、証明するときによく使うのが「漸化式」です。
では、a^+b^nに関する漸化式はどうなるでしょう?
漸化式を作ってみよう
作り方は簡単です。
a^n+b^nに対して、基本対称式であるa+bとabを利用して、少し次数を下げながら等式をつくります。
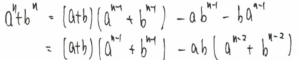
ここで、登場するのが、n-1乗の部分と、nー2乗の部分です。
つまり、n乗と、nー1乗と、n-2乗の3つの部分の関係式(3項間漸化式)が登場するということです。
3項間漸化式に対して使う漸化式は、普通の帰納法ではなくて、強化帰納法です。ということで、a+bとabの値が欲しくなります。
それが、(1)の問題です。
つまり(1)は、(2)で強化帰納法を使う際に出てくる漸化式を作るために必要な値を求めさせる、誘導問題だということなのです。
(1)対称式から基本対称式を求めよう
では、(1)を見てみましょう。
普通の対称式の問題より、少し計算が面倒なだけで、本質はただの連立方程式の問題です。
a^2+b^2と、a^3+b^3の両方を、基本対称式で表し、加減法や代入法で一つずつ求めるだけですね。
これに関しては、あとで手書きの解答を見てください。
(2)漸化式を使えば、非常に簡単
そして(2)ですが、強化帰納法に、求めた値と漸化式を代入すれば、難しいところが全くありません。
「4の倍数と4の倍数を足したら、4の倍数になる」という、至極当たり前な事実を、わざわざ帰納法の中で示しているにすぎません。
ということで、手書きの解答をご覧くださいませ。
まとめ
今日は、次回以降の導入編。
強化帰納法や、3項間漸化式を自分で作る技術などが、東大では非常に大事で頻出です。
よく復習してから、次回以降の問題をごらんくださいませ。




