2019年東大理系数学(第3問)入試問題の解答(答案例)・解説(2)(空間図形、平面で切断)
目次
◆日本一徹底して東大対策を行う塾 東大合格「敬天塾」
弊塾のサービスは、全てオンラインで受講が可能です。
地方の方、仮面浪人の方、社会人受験の方など、広く皆さんにご受講いただけます。
ご希望のサービスを、以下からお選び下さい。
【万全の東大受験対策をしたい方】
≪東大文系受験者対象≫敬天塾プレミアムコース生徒募集はこちらから
【敬天塾について知りたい方】
敬天塾の理念
敬天塾からの東大合格者インタビュー(ノーカット)はこちら
東大生や東大卒業生への指導依頼はこちら
2019年 東大数学 理系第3問(2)
では、昨日の(1)の解説に続きまして、(2)の解説に行きましょう。
切断面は何角形?
(2)の問題は、切断面が八角形になるpの範囲を求めよというものです。
(1)が大きなヒントになっているのですが、お気づきになったでしょうか?
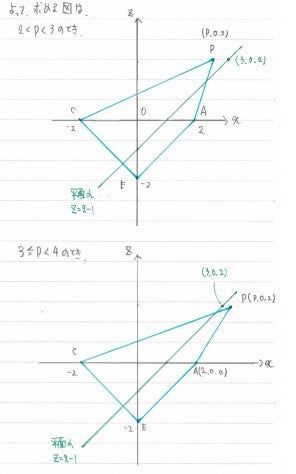
まずは、(1)の結論の図をもう一度ご覧ください。
点Pに対して、左側を平面αが通るか、右側を通るかで場合が分れています。
そして、これが八角形になるかならないかの境界線になるのです。
どういうことでしょうか?
平面と直線の共有点は、点
これも(1)と同様、空間図形の基礎的な考え方を使います。
平面と直線の共有点は、点になるというものです。
(1)の結論の図は、y=0の切断面のみを表していますが、本当は八面体です。八面体には12本の辺がありますから、そのうちいくつかを平面αが切断しているはずです。
ということで、(1)の図に、書かれていない八面体の辺(をy=0に射影したもの)を赤色で書き込んでみました。実際には、紙面から手前向きの辺と、奥向きの辺があるのですが、対称性からy=0上では1本の線分に見えています。
(y=0上にある辺は青色です。)
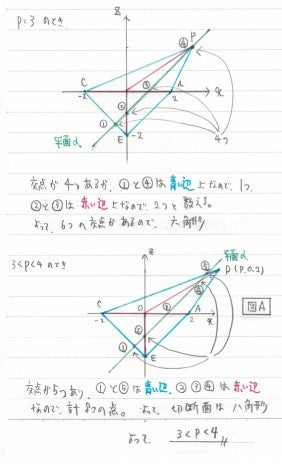
例えば、2<p<3の場合はこちらです。
平面αが、①②③④と4回八面体の辺と交わっているのがわかるでしょうか?
このうち、①と④は青色(y=0上の辺)の交点で、②と③は赤色(y=0上にない辺)との交点です。
①と④はy=0上で平面αと交わっているから数え方は簡単なのですが、②と③はそうはいきません。②と③は対称性からy<0とy>0に1つずつ交点があるはずなので、2つ分と数えます。
つまり、1+2+2+1=6となり、切断面は6角形であることが分かるのです。
これを、p=3の時と、3<p<4の時でも書いてみると、
p=3では6角形、3<p<4の時は八角形になることがわかります。
よって、(2)の答えは3<p<4となるのです。
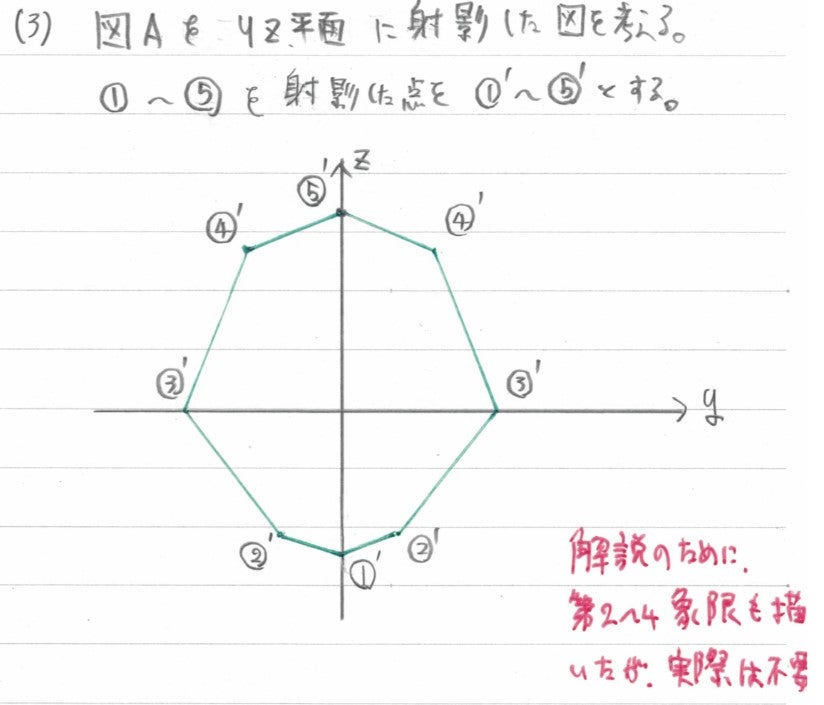
ちなみに、先取りして(3)の序盤をお見せすると、x=0に射影した図はこのようになり、確かに八角形であることが分かります。
立体的に考える方が難しい
ということで、答えが出たわけなんですが、立体的な図を描いて、切断面が8角形になることを理解することはできるのでしょうか?
もし実物大のものを用意して、カッターか何かで切断したら一番わかりやすいのでしょうが、入試会場ではできません。
やはり、頭の中にイメージするか、計算用紙に「立体的な図」を描いて考えるしかありません。
僕も、手書きの解答を作るときに、あれこれ試して描いてみたんですが、どうにも上手く示せずに時間を浪費しましたし、読者の皆様に分かりやすいような図に仕上がりまっせんでした。
やはり、立体は平面図形に切断して、その上で考える方が良いのでしょう。
切断自体は小学生や中1で習う技術なのですが、奥が深いものですね。
ということで、明日は(3)に参ります。
◆日本一徹底して東大対策を行う塾 東大合格「敬天塾」
弊塾のサービスは、全てオンラインで受講が可能です。
地方の方、仮面浪人の方、社会人受験の方など、広く皆さんにご受講いただけます。
ご希望のサービスを、以下からお選び下さい。
【万全の東大受験対策をしたい方】
≪東大文系受験者対象≫敬天塾プレミアムコース生徒募集はこちらから
【敬天塾について知りたい方】
敬天塾の理念
敬天塾からの東大合格者インタビュー(ノーカット)はこちら
東大生や東大卒業生への指導依頼はこちら