2019年東大理系数学(第3問)入試問題の解答(答案例)・解説(3)(空間図形、平面で切断、射影)
◆日本一徹底して東大対策を行う塾 東大合格「敬天塾」
弊塾のサービスは、全てオンラインで受講が可能です。
地方の方、仮面浪人の方、社会人受験の方など、広く皆さんにご受講いただけます。
ご希望のサービスを、以下からお選び下さい。
【万全の東大受験対策をしたい方】
≪東大文系受験者対象≫敬天塾プレミアムコース生徒募集はこちらから
【敬天塾について知りたい方】
敬天塾の理念
敬天塾からの東大合格者インタビュー(ノーカット)はこちら
東大生や東大卒業生への指導依頼はこちら
2019年 東大数学 理系第3問(2)
では、(1)の解説、(2)の解説に引き続き、(3)に行きましょう。
今度はx=0に射影する
(1)と(2)ではy=0に射影しましたが、今度はx=0に射影する問題ですね。座標平面上で(y、z)となっていて、ここから読み取れます。
ということは、(2)の答えを出すときに描いた図が、とても役立ちます。
再掲しましょう。こちら。
ちょっと見づらいですが、①~⑤の5つの交点があり、①と⑤は青色(y=0上で)の交点、②~④は赤色(y=0上にない)交点でした。
この図Aをx=0に射影して、y≧0かつz≧0の部分の図を描けばよいという問題です。
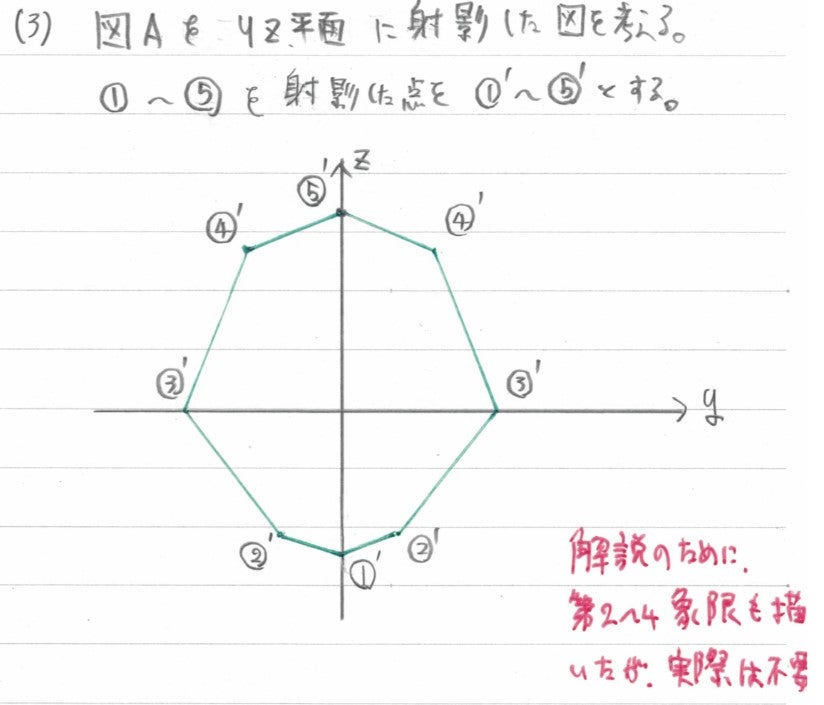
解答を描く際には不要なのですが、分かりやすい解説のために、zy軸全体で図を描いてみました。①~⑤を射影した点を①’~⑤’としています。
ほら、確かに八角形でしょう。(本当の断面ではなく、射影後なのですが)
このうち、第1象限の部分だけ取り出して、面積を求めれば答えです。
射影前の座標を求めて、射影する
では、第一象限の面積を求めていきましょう。
そのためには、③’、④’、⑤’の座標が分からなければなりません。ということで計算を進めていきましょう。
まずは⑤’ですが、(2)の答えの図を使って求めます。
まずは⑤.
この図において、⑤の点はy=0上にありますから、射影後のy座標も0(確かに八角形のてっぺんにあります)
z座標に関しては、直線の交点として求めればよいので、直線CPと、平面αを連立して求めてください。
次に④ですが、y座標がわかりません。y=0でないことだけはわかってますが、具体的な値は不明。
よって、面倒ですが、ベクトルの直線の方程式を使って求めます。
最後③は、ほとんど計算が要りません。なぜなら、③は点M(N)そのものだからです。(平面αは辺ABと辺ADにおいて、中点M(N)を通るというのが定義です)
つまり、M(1,1,0)をx=0に射影して(y、z)=(1,0)です。
これを書き込んだら、あとは面積を計算するだけ。別に難しいところはないので、一気に手書きの解答をご覧ください。
(1)からの分全てを掲載します。
いやいや、それにしても難しい問題でしたね。
空間図形の問題って、解説記事を書くのにめちゃくちゃ時間がかかるんですが、今回のは最長記録だったと思います。
実際は、中学生の計算だけで解けてしまうところが、またいやらしい問題。さすがの東大クオリティだったと思います。
射影や空間図形の話題は苦手にする人がとても多いので、ぜひよく復習してください。
では、明日からは、通常通り1日1問のペースに戻します。
◆日本一徹底して東大対策を行う塾 東大合格「敬天塾」
弊塾のサービスは、全てオンラインで受講が可能です。
地方の方、仮面浪人の方、社会人受験の方など、広く皆さんにご受講いただけます。
ご希望のサービスを、以下からお選び下さい。
【万全の東大受験対策をしたい方】
≪東大文系受験者対象≫敬天塾プレミアムコース生徒募集はこちらから
【敬天塾について知りたい方】
敬天塾の理念
敬天塾からの東大合格者インタビュー(ノーカット)はこちら
東大生や東大卒業生への指導依頼はこちら