2019年東大文系数学（第3問）入試問題の解答（答案例）・解説（確率、多角形グルグル、道順、中学受験で解ける）

２０１９年　東大数学　文系第３問

では、今日は文系第３問です。復活した確率の問題。

確率の問題は、設定の読み込みに１０分かけても良い

東大の確率だなぁっていう問題。 知らない設定が登場し、読み込んでカラクリを解き明かすのに時間がかかる。 複雑な場合分けが登場し、立式までに時間がかかる。でも計算はそれほど面倒ではない、といったところ。   ということで、うちの塾では「確率の問題が出たら、１０かけてよいから設定の読み込みをせよ」と教えています。   さて、今回のカラクリやいかに！？

（１）は簡単。

（１）は簡単ですね。１０回コインを振って、またＡに戻ってくるという問題です。 １周するかどうか、１周するとしたら、右回りなのか、左回りなのか、という場合分けになりますが、これは簡単に理解できるでしょう。 これは受験生ならば解けなければならない問題ですね。解説は割愛。手書きの解答をご覧くださいませ。

（２）は場合分けが複雑

次は（２）の問題なのですが、これはかなり複雑です。 Ｔ「Ｆに少なくとも１回立ち寄る」という条件が加わりますが、これを処理するためには、複雑な場合分けが必要です。   版時計周りだとしたら、５回目にたどり着くか、７回目にたどり着くか。でも７回目にたどり着くとき、５回目にはＦに移動してちゃいけないから・・・。 などと考え始めると、混乱してしまいます。   実際は、文系受験者にとって、これはかなり難しかったのではないかと思いますね。恐らく（１）だけ解いて、（２）は０点のような答案が多いのではないだろうかと思います。

ビジュアル化①　マス目を作る

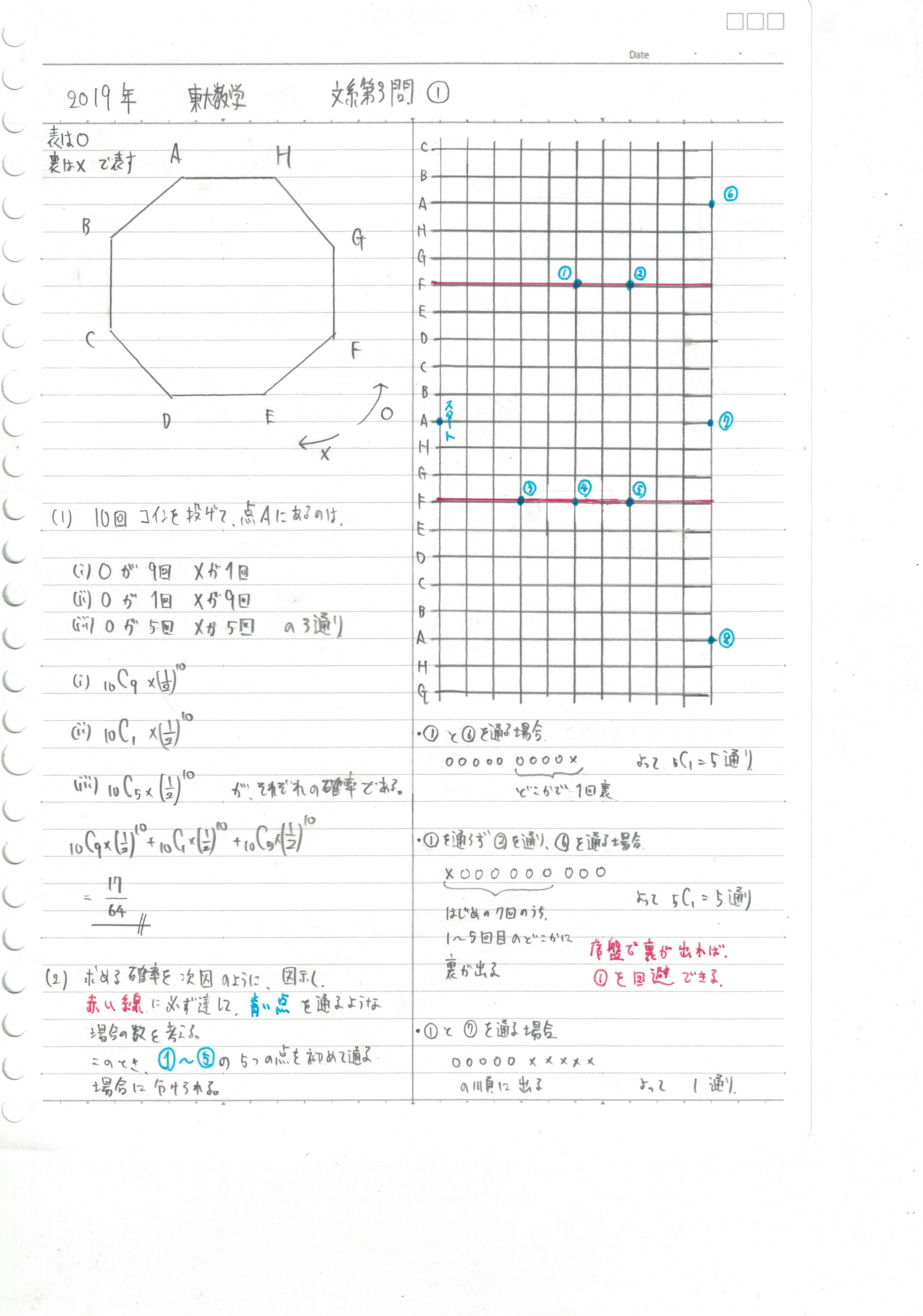
予備校の模範解答では、場合分けを駆使して解いているものがありましたが、僕が読んでもあまり意味がわからない解答だったので、分かりやすさを重視して、２つビジュアル化した解答を用意しました。 （といっても、受験生が時間内にこれを思いつくかどうかは、微妙なのですが）   一つ目は、下のようなマス目を作って、道順の移動で考える方法です。   スタートのＡの位置から、①～⑤のどこかの点（Ｆ）を通り、⑥～⑧の点（Ａ）に辿りつくという場合分けです。 このようにマス目を作ると、一気に見やすくなりますね。今回は正八角体をグルグルする問題でしたが、多角形をグルグルする問題は良く出ますから、他の場合にも使ってみてください。 ※ただし、①～⑤は「初めてＦに到達する」という条件の下で場合わけします。   これで場合分けができますので、あとは計算して終わりとなります。

ビジュアル化②　中学受験方式

次は、中学受験で習う方式で計算するものです。 普通、このような道順の問題の場合、コンビネーション（ｎＣｒ）で計算するのが一般的ですが、パスカルの三角形を利用して、足し算を繰り返す方法もあります。   まずは、通れない道をすべて消して、通れる道だけを残します。 そして、ある点に対し、一つ前タイミングにいる点の数字を２つ足しながら、ゴールにたどり着くのです。 すると、ゴールへの生き方が２０６通りになります。   あとは、２＾１０で割って、（１）の答えから引けばＯＫ。   ということで手書きの解答をご覧くださいませ。 場合分けが難しいのですが、工夫をすると簡単になるというのも東大っぽい。 多角形グルグル問題は、このマス目の作り方を覚えておくと使えますよ。  

敬天塾作成の解説

こちらのｐｄｆファイルは無料でダウンロードいただけます。
受験生の学習はもちろん、先生方の授業にお役に立てるのであれば、どうぞご自由にお使いください。
断りなしに授業時にコピペして生徒に配布するなども許可していますが、その際「敬天塾の答案である」ということを必ず明記していただくようお願いします。
ただし、無断で転売することは禁止しております。何卒ご了承ください。