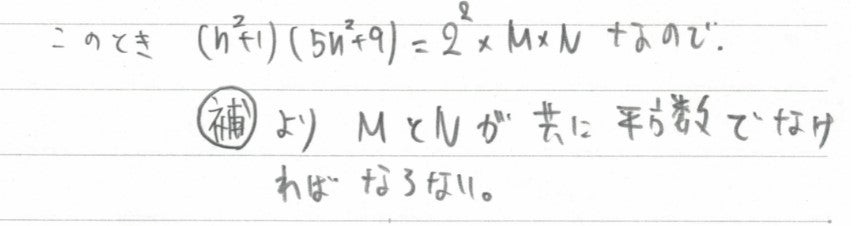2019年東大理系数学(第4問)入試問題の解答(答案例)・解説(整数、最大公約数、ユークリッドの互除法)
目次
◆日本一徹底して東大対策を行う塾 東大合格「敬天塾」
弊塾のサービスは、全てオンラインで受講が可能です。
地方の方、仮面浪人の方、社会人受験の方など、広く皆さんにご受講いただけます。
ご希望のサービスを、以下からお選び下さい。
【万全の東大受験対策をしたい方】
≪東大文系受験者対象≫敬天塾プレミアムコース生徒募集はこちらから
【敬天塾について知りたい方】
敬天塾の理念
敬天塾からの東大合格者インタビュー(ノーカット)はこちら
東大生や東大卒業生への指導依頼はこちら
2019年 東大数学 理系第4問
(1)は東大らしく、ユークリッドの互除法
(1)から早速、東大らしさが全開の問題です。
大好物の「最大公約数」の問題。当然「ユークリッドの互除法」を使います。
「当然」と書きましたが、「え?そうなの?」という人のために少し書いておくと、新課程になり「ユークリッドの互除法」が指導範囲内になった瞬間から、東大では超頻出問題になりました。
過去問を参照すればわかります。
キーワード「最大公約数」から連想しよう
また、「最大公約数」というのも、超キーワード。
最大公約数に関連する問題は、主に2パターンしかありません。
一つ目は「ユークリッドの互除法」を利用するパターン。
もう一つは、最大公約数をg、最小公倍数をlを置き、4式1条件を作るパターンです。
具体的には、aとbの2整数に対して
・a=a’g (式①)
・b=b’g (式②)
・l=a’b’g (式③)
・ab=gl (式④)
・a’とb’は互いに素 (条件①)
という、4式と1条件です。
これを色々いじって求めるパターンもあります。
ただし、東大で「最大公約数」が登場したら、まず「ユークリッドの互除法」を疑ってよいでしょう。それくらい偏って頻出です。
(1)は瞬殺!
では、(1)に互除法を利用してみましょう。
すると、簡単にn^2+1と、4の最大公約数を考えればよいことが分かります。
4には約数が1と2と4しかないので、ここで3択です。
また、素因数が2だけですから、2の剰余類で場合分けするのも自然な発想。
ということで、偶数(2の倍数)と奇数(2の倍数でない)で場合分けをすると答えです。
とても自然な流れで答えが出ました。
(2)平方数の処理
次は(2)
さっき、最大公約数を求めた2数が、掛け算されていますね。そして、全体が整数の2乗にならないことを示せというもの。
ここで登場した、「整数の2乗で表せる数」のことを「平方数」と言います。
さて、2つの数の積が平方数になためには、どのような条件が必要でしょうか。
教科書や、参考書ではあまり類題を見たことがないでしょうから、受験生にとっては難しかったと思います。
ここでは、
補題「互いに素なxとyについて、xyが平方数⇔xとyがともに平方数」
という性質を使って解説しようと思います。
偶数の場合
(1)の結論として、偶数と奇数で場合分けをしたので、(2)でも場合分けをしましょう。(誘導に乗ります)
nが偶数の場合、命題①により2数はともに平方数となりますから、
n^2+1も、5n^2+9も平方数となるはずです。
しかし、n^2+1は絶対に平方数になりません。
手書きの解答では、ちょっと「ウマイ」方法で解説を書きました。
これなら、2行くらいで証明できるので簡単です。但し「ヒラメキ」に頼った解法に見えてしまうかもしれないので、もう一つご紹介します。
例えば、n^2+1=k^2(kは整数)とおいて、kが存在しないことを示す、という方針でも良いと思います。
このとき、n<kであり、(nーk)(n+k)=1 と因数分解できます。
しかし、1というのは、1×1か、(-1)×(-1)しか、積の候補がありません。
だから、nーk(小さい数)と、n+k(大きい数)の積が1になることはありません。
よって、このようなkは存在せず、n^2+1は平方数でないことが示せます。
最大公約数だから、4式1条件を作ろう
では、難しそうな奇数の場合。
と言っても、実は基礎の積み重ねで解くことができます。
というのも奇数の場合は最大公約数が2となりますが、
先ほども書いた通り最大公約数と言われたら、
①ユークリッドの互除法
②4式1条件を作る
という2方針しかありません。
ユークリッドの互除法は先ほど使ってしまったので、今度は4式1条件を作るのです。(手書きの解答では、結果として不要なので2式1条件しか載せていませんが、実際に解答を作る上では立てた方が良いです。)
ここまでは定石の手段。
そこで、2数の積を取ってみると、結局MとNがともに平方数でなければならなくなります。
ここまでは、何も不思議なことは起こっていません。最大公約数と言われたから、最大公約数の条件式を立てただけです。
発想力(難)5の剰余類で矛盾を示す
ここからは、解答が分岐するところ。
正直なことを言えば、理Ⅰや理Ⅱであれば、これ以降は解けなくても良い気がしますが、解説は書きます。
恐らくこの時点で式をゴチャゴチャいじて、色々試すのでしょう。
その中には、5n^2+9=2Nにn=2m-1を代入した式も登場すると思いますが、ここに注目してみました。
すると、Nの右辺に係数の10が登場します。
これに注目して、5を法とする合同式を取ってみると、Nが平方数でないことが証明できます。
発想が難しいので、(2)の前半までしっかり解答を描ければOKでしょう。
では、全体の解答です。
今回の数学の問題の中では、難しい問題になるのではないかと思います。
但しそれは満点を取る前提での話で、20点中10点を取るのは非常に簡単な問題。(12~13点くらいかも)
この部分点をしっかりとれるかどうかが、運命の分かれ目でしょう。
◆日本一徹底して東大対策を行う塾 東大合格「敬天塾」
弊塾のサービスは、全てオンラインで受講が可能です。
地方の方、仮面浪人の方、社会人受験の方など、広く皆さんにご受講いただけます。
ご希望のサービスを、以下からお選び下さい。
【万全の東大受験対策をしたい方】
≪東大文系受験者対象≫敬天塾プレミアムコース生徒募集はこちらから
【敬天塾について知りたい方】
敬天塾の理念
敬天塾からの東大合格者インタビュー(ノーカット)はこちら
東大生や東大卒業生への指導依頼はこちら