2019年東大文系数学（第4問）入試問題の解答（答案例）・解説（ベクトル、領域図示、１文字固定）

２０１９年　東大数学　文系第４問

なんと、３連続でベクトルの領域図示の問題が出ました！これは驚き。 これまで入試では、それほど頻出で扱われなかったタイプの問題でしたので、今後、問題集などで例題や類題が増えるでしょう。 では、詳しくみていきます。

有名な図形の図示

まずは、領域Ｄ、つまり　｜ｘ｜＋｜ｙ｜≦１の領域図示ですが、これは即答したい問題。超有名な領域です。   ちゃんと書こうとすると、ｘの正負と、ｙの正負によって４つの場合分けをすればよいでしょう。 但し、僕の解答では、ｘとｙに関して偶関数になっていることを利用して簡潔に書きました。 このように、ダイヤモンド型になるのです。 これは、解けないとマズイ問題。さっさと書いて、次に行きましょう。

動点が２つあるときは、１つ固定

次に、領域Ｅの図示に入ります。 点Ｐと点Ｑが領域Ｄを動き、ＯＰベクトルとＯＱベクトルの差を取ったベクトルの通過領域を求める問題です。   さて、この問題のややこしいのは、点Ｐと点Ｑが動くところです。つまり動点が２個あるというところ。 このような問題が登場したら、鉄則があります。 「動点が２つあったら、１つを固定せよ！」   これは、数学において、非常によく使う技法です。

２変数関数も、１つ固定

ちょっと脱線して、同じように２つ動くものがあった時に、１つを固定して考える典型問題をご紹介しましょう。 恐らく、多くの高校生にとって、初めて登場するのがこのタイプの問題でしょう。   （青チャートⅠＡより）   ｘとｙの両方が変数の時、はじめどちらかを定数とみなして１変数関数と見ながら最大値（最小値）を求め、固定した文字を変数に戻して最大値（最小値）を求めます。   ２つ動くものがあったら、１つ固定。 しっかり覚えておきましょう。

領域Ｅを描いてみる。

ということで、点Ｐと点Ｑのどちらかを固定して領域を考えてみましょう。 分かりやすい方を選び、点Ｑを固定してみました。 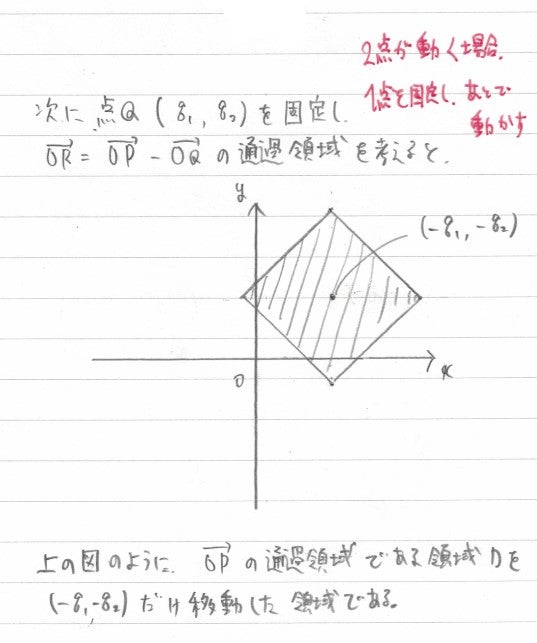  すると、上の図のように、点Ｑを領域Ｄにおいての原点とみなしたような、ダイヤモンド型の領域が描けます。

固定した点を動かす

さて、この次は、先ほど固定した点Ｑを動かします。 つまり、ダイヤモンドの中心（点Ｑ）を、ダイヤモンド（領域Ｄ）の形に動かすのです。 すると、このような形になり、領域Ｅの完成です。    

（２）は記述が難しい！

さて、次は（２）の問題ですが、これは簡単ともいえるし、難しいともいえる、珍しいタイプの問題。 予備校の判定では簡単な問題に判定されるかもしれませんが、僕は結構難しいと思います。   では何が難しいかというと、「記述するのが難しい」のです。 東大では、現代文や古文、漢文などを中心に、「何となく頭では分かっているけど、言語化しようとすると難しい」という問題が出ますよね。   この数学の問題も、同様。 言われてみれば、（１）と同じ領域になりそうだけど、どうやって記述して証明すればよいかわからない、という問題です。

具体的にして、記述する

このような場合、どうするかというと、一定の方法論があります。 具体的にして証明するのです。   今回は、点Ａ（ａ、ｂ）とおき、ＯＳベクトルと、ＯＴベクトルを表現します。 すると、ＯＵベクトルが自然と、（１）と同じように表現できて終わり。   言われてみれば簡単だけど、自分で書こうとすると困ってしまう問題ですね。 では、手書きの解答です。 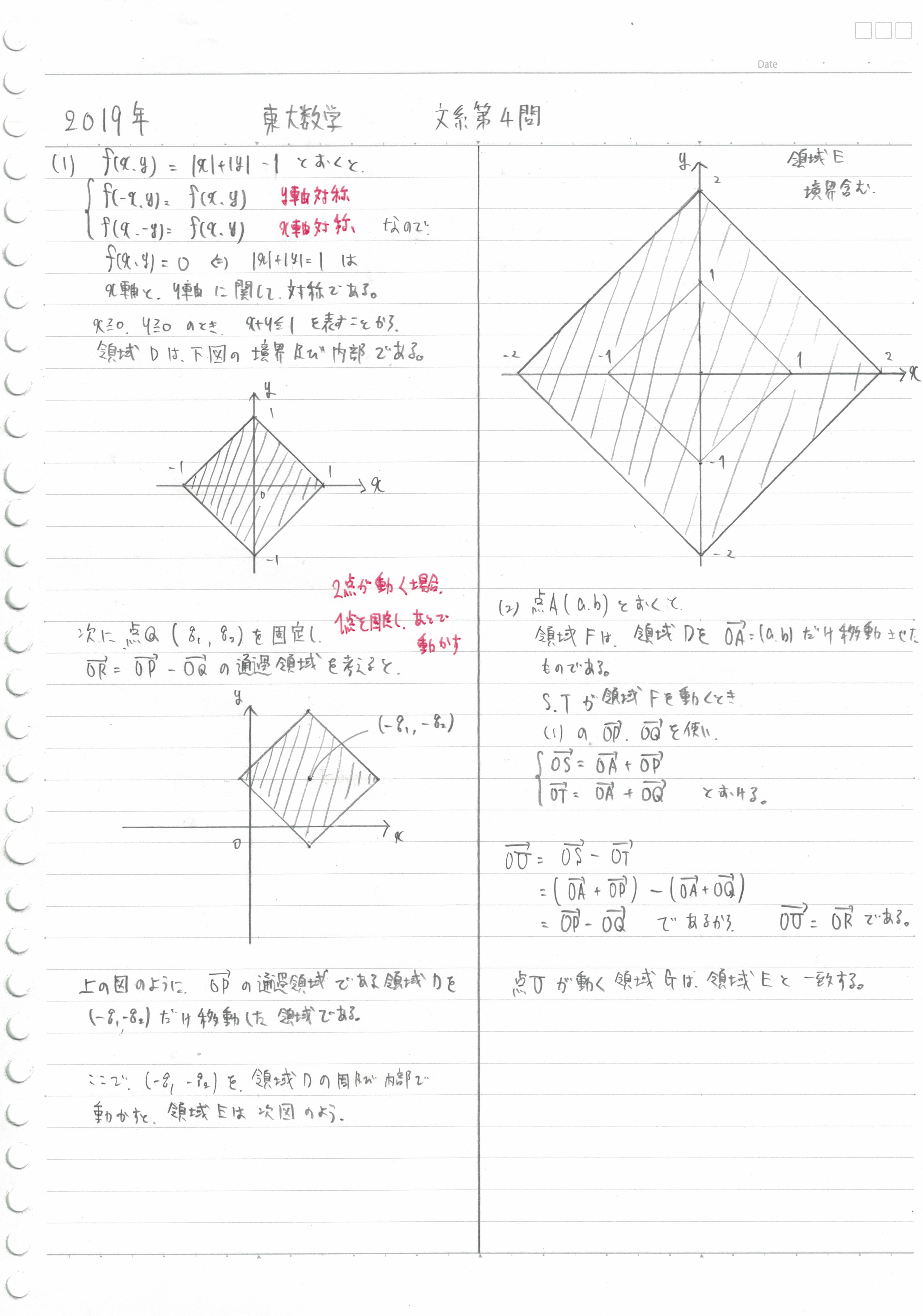    はじめのダイヤモンド型の領域までで終わってしまった受験生も多かったような気がしますが、数学の基本的な考え方はあまり多くありません。 基礎の積み重ねで、応用問題が解けます。ぜひ、直感ではなく、方法論に基づいた勉強を続けてください。  

敬天塾作成の解説

こちらのｐｄｆファイルは無料でダウンロードいただけます。
受験生の学習はもちろん、先生方の授業にお役に立てるのであれば、どうぞご自由にお使いください。
断りなしに授業時にコピペして生徒に配布するなども許可していますが、その際「敬天塾の答案である」ということを必ず明記していただくようお願いします。
ただし、無断で転売することは禁止しております。何卒ご了承ください。