２０１９夏　河合東大オープン　文系数学第１問の解説

2019年夏　河合東大オープン　文系数学第１問の解説

毎年恒例、東大模試の解説を始めていこうと思います。
昨日実施された、河合オープンの文系第１問です。
まず問題から。

（１）は教科書例題レベル

瞬殺です。
（１）は教科書例題レベルと言ってよいでしょう。

関数の問題の超基本事項（中２で習います）である
関数の交点　⇔　連立した方程式の解
を使って、とにかくＣ１とＣ２を連立。すると、定数ｋが右辺に分離出来て、左辺が３次関数となります。

あとは増減表書いて、グラフを描いて、３回交わるｋの範囲を求めると。
まさに教科書例題です。

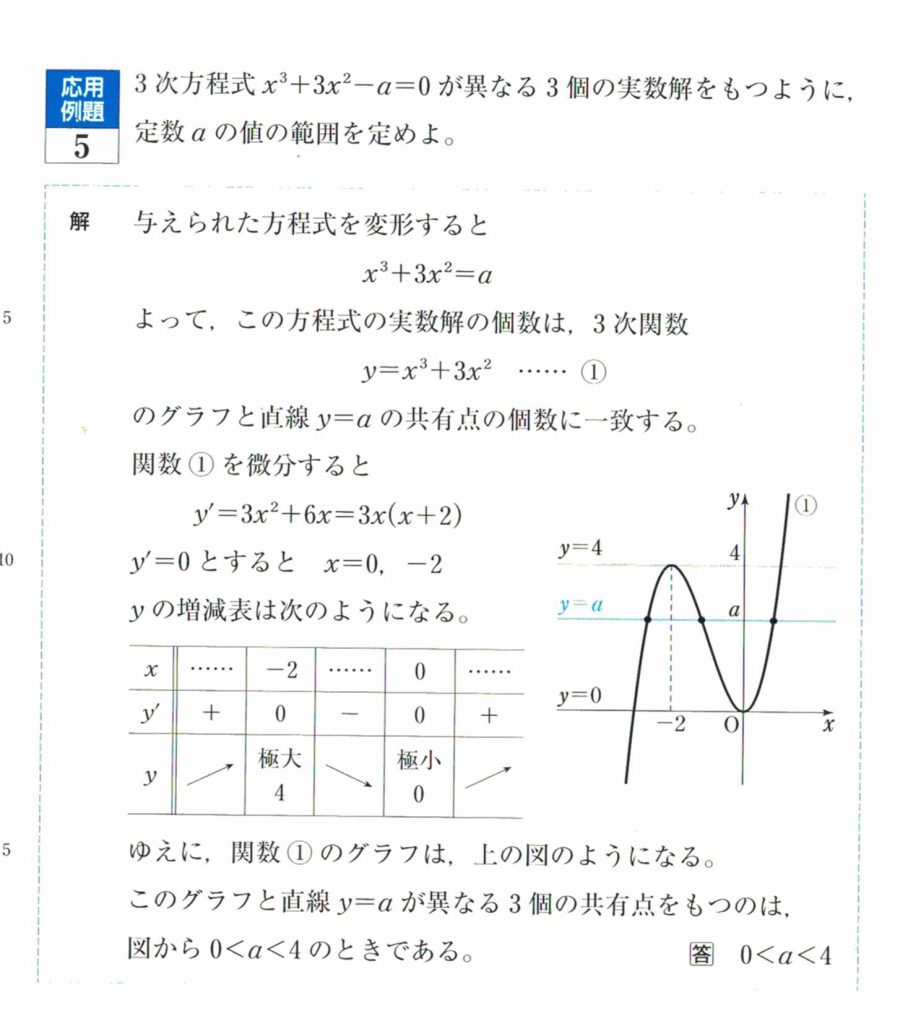
↑この教科書の例題と同じ問題です。

さすがに、これは解けなきゃ。

（２）はも瞬殺

（２）は教科書例題レベルとは言いません。しかし、教科書レベルではあります。

α＋β＋γという数式はどこで見たことがあるでしょうか？端的に行って「解と係数の関係」の時だけでしょう。３文字の和という意味であれば、因数分解の公式など、他のものもありますが、今回は交点のｘ座標の和です。
先ほども言いましたが、交点のｘ座標というのは、方程式の解です。
つまり、３つの解の和ですから、３文字の解と係数の関係で一択になります。

というのが分かってしまえば、あとは鼻息交じりで、連立して３次方程式を作って解と係数の関係を立てておけば終わり♪
これも瞬殺で、ラスボスにチャレンジしましょう。
数学が得意なら、ここまでで３分以内でたどり着きたい問題。

垂心は扱いが雑でよい

では、最後に（３）に行きましょう。
簡単に言うと、△ＡＢＣの垂心の軌跡を求めろという問題。
軌跡の問題は、その点の座標をパラメータで表し、消去してｘとｙの関係式を求めるだけです。
但し、その計算過程で、少し図形的な考察を加えると簡単に行くこともあります。（アポロニウスの円など）

では、垂心はというと「何もなし」。
はっきり言って、垂心なんてその程度「イジって」おけば十分。いや、イジッたところで何もでてきません。
外心なら正弦定理と組み合わせるとか、重心なら２：１に内分するとか、色々あるのですが、、、。
垂心に関しては、ただ単に頂点から垂線を下ろしたら垂心を通るというだけで、特に何も覚えることはありません。

ということで、安心して各頂点から垂線を下ろしておきます。

垂線を下ろして、パラメータを消去

直線ＡＢの方程式を求めたり、点Ｃから垂線を下ろしたりと計算を進めると、それなりに複雑な式が出てきますが、ここからはただの「計算力勝負」

こういうときは、自分が立てた式を箇条書きにしておいて、使える「武器」（つまり式）をはっきりさせておくのが良いでしょう。
今回の問題は、解と係数の関係の３本がパラメータ消去に使える式です。
これを念頭に置きながら、そして何度も計算ミスや遠回りをしても良いから、最後まで計算し終わったら終了です。

ちなみに、αとβとγとｋは、それぞれが関係のある文字なので、１つになるまで消去しなければいけません。
そして、αとβとγはそれぞれ対称性がありますから、１つが消去できるということは３つが消去できるということ。
こういうことを冷静に考えられると、ｋを残すのが正解だとわかります。

ということで、手書きの解答です。

まとめ

（３）の計算が面倒くさく、慣れてないと混乱してしまうのでしょうが、流れ自体は一文字も書かなくても読める問題です。
（１）や（２）は満点を取らなければならない問題ですから、（３）の部分点も含めて１０点以上はほしいところ。
東大の本番の入試の難易度と比べても、それほど違いはないと言えるでしょう。
では、また次回