【世界一早い東大模試解説】2017夏 駿台実戦 文系数学の作戦
2017夏 駿台模試
4問を並べて作戦を考えよう!
昨日に引き続き、東大模試の作戦考察をしましょう。
昨日も書きましたが、簡単に趣旨だけ。
いつも一問ずつ復習して、解説を聞くことはありますが、入試を攻略しようとしたら、一年分の問題全体でバランスを考えなければなりません。
試験開始の合図の直後、問題の初対面の状態から、どう考えて、どう時間を使えば点数が最大化されるか、考えてみましょう。
それぞれ一問ずつの解説記事は下のリンクから見れます。
【世界一早い東大模試解説】2017夏 駿台実戦 文系第3問(存在領域、ベクトル)
他の東大模試に関連する記事はこちら。
東大の過去問題の解説はこちら
問題冊子を開いたら、こう考えよう。
それでは本題。
試験時間100分の開始数分で、まず4問ともに目を通しましょう。
特に、今回の駿台模試では、ここに鍵がありました。
【第1問】
シンプルな問題。
解法のパターンも、よく勉強している方なら2パターンしかない(細かくは3パターン)と分かるでしょう。
①割り算する
②合同式(mod)で解く
③二項定理で解く
但し、大抵の場合は二項定理で解くより、合同式で解く方が手数が少なく、解答もシンプルに終わる場合が多いです。
また、余りの問題は、結局は規則性の発見です。
6を1乗から5乗、10乗として見て、あまりが同じになる所が発見出来れば終わり。
解答の方針も立てやすく、複雑すぎる計算がなさそうなので、いきなり手を付けられる問題。
【第2問】
円の上に点を打ち、三角形や四角形を作るのは、よくある問題。
だけど、求める条件が「鋭角三角形の3頂点を含む4点を選ぶ確率」という、珍しい条件。
当然、こんな確率求めた事ないので、急に解法が思いつかないはず。
ただ、(1)は正6角形で、(2)は正8角形ですから、あまり複雑な図形も登場しません。
まあ、手が付かないことはないだろう。少なくとも部分点はもらえそうかな、と思える問題。
1問目に解く問題ではないかもしれないけど、優先順位は高めで良さそう。
【第3問】
パッと見で気付くポイントとしては、
①対称性がある
②三角関数がある
③xとyの範囲が限定されている
④存在領域の図示の問題
ということでしょう。
対称性に注目して変形すると、キレイな形になりそうかな。(暗算が得意であれば、2乗して和を取ると、cosの加法定理が出る事が予想出来ます。)
あとは、xとyの定義域に注意して、解を持つ条件で攻めれば行けるのか?
一応、手を付けられそう。部分点は来るだろうか・・・。
※但し、この問題は、初対面の印象で、上のように判断して解くと痛い目を見る問題でした。詳しくは、こちらのリンクに書いてあります。
実際は、存在領域からベクトルを連想して解くのがベストな問題です。ご注意を。
【第4問】
3次関数と2次関数があって、異なる3つの交点を持つ。
面積を計算すると、5:32になる。
別に、特段難しい条件は出てきません。
(1)でbをaで表すって事は、文字が一つ減るって事。
(2)では、aを変化させて、通過領域って事は、解の配置で解けそう。
とりあえず図を描いて、積分計算をすれば出来そう・・・。これも部分点は来るだろうな。
※これも、やってみると痛い目を見る問題。
問題としてはシンプルですが、計算が厳しくて、途中で挫折する可能性大。
初対面では優しそうですが、付き合ってみると怖い。
解く順番
以上、第1問から第4問まで見てきましたが、解く順番としては、第1問が始めで良いでしょうね。
初手から最後までが、何となく予想出来る問題は第1問と第4問。
そのうち、計算量が少なく処理出来そうなのは、第1問です。
よって、始めの2問は、1⇒4で決まり。
第2問と第3問ですが、どちらが優先かは、好みで良いレベルの差でしょう。
第3問で、まず式変形をしていじって見たければ、そちらでも良いですし、第2問で確率を求める条件を考えても良し。
好きな方からやってみて下さい。
但し、第4問で計算が激しくなった辺りで注意。
積分計算や、高次方程式の計算が激しくて困るはずです。その時深追いせず、次の問題に切り替えれるかが重要でしょうね。
結果論ですが、第2問が解きやすい問題です。第4問に時間をかけすぎて、第2問に時間を掛けられないのが怖いです。
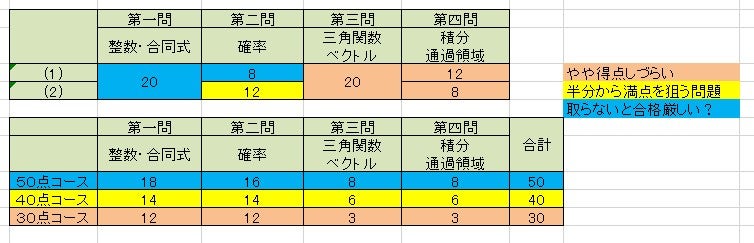
目標に対する、各設問の得点例
では、今度は、目標得点別の得点例です。
独断と偏見で、難易度と配点を決めています。参考にとは思いますが、参考以上にするのはオススメしません。
第3問は、発想が得にくいということで、難問指定。
第4問は、問題は簡単だけど、計算が難しいということで、難問指定です。
この2問の合計40点中で、10点とれたら十分でしょう。第1問と第2問でしっかり取れるかどうかが最大のポイントです。
逆に、第1問と第2問は満点を狙える問題。
上の図は、満点は避けて作ってますが、気持ち的には満点を狙いたいところです。
2016年や2017年の本番の東大入試よりも、難しいと思います。
40点取れたら、十分すぎるくらい合格ラインだと思います。
【告知】