2020年東大理系数学(第2問)入試問題の解答(答案例)・解説
2020年東大数学 理系第2問
さあ、出ましたよ。
斜交座標の問題です。
ここ3年くらい、ベクトルの領域図示の問題が出ていましたが、今年も似ている問題が出ました。
ただ、解くだけだったら、ベクトルを使わず、平面幾何的に解いた方が簡単ではありますが。
では、問題を見ていきましょう。
三角形の形が決まらない
問題を読んでいて、全員引っ掛かったのが、「△ABCの面積が分かっているのに、形が分からない」というところでしょう。
そして、よく読んでみると、「点Xの通過領域の面積を求めろ」ということですから、どうやら△ABCの形はあまり関係ないようです。
(一応、△ABCの形によって場合分けをしながら面積を求める可能性もありますが)
これに似ているのは、「位置ベクトル」でしょう。
△ABCが与えられて、内分点や外分点などの点を定義して、交点を求めるような問題があると思いますが、これは元々の△ABCの形は関係なく、点の位置が定義できます。
また、
【例題1】
(OPベクトル)=s(OAベクトル)+t(OBベクトル)
の時に、s+t=1を満たすと、点Pの動く場所はどこでしょう?
というような問題がありますが、これも点O、A、Bの場所には関係なく、答えがでます。
斜交座標をマスターせよ!
さて、さきほどの【例題1】の問題を解く際に「斜交座標(しゃこうざひょう)」という考えを導入すると解きやすくなるのをご存じでしょうか。
直交座標は、x軸とy軸を直交させ、x座標とy座標の数字によって点を定めるというものです。
これに対して、斜交座標は、2つの軸が斜めに交わっているタイプです。
上の【例題1】でいうと、OA方向と、OB方向にx軸やy軸のような軸が伸びているようなイメージで解くことになります。
さて、斜交座標が何となくわかったとすると、この問題の考え方や理解が深まると思います。
今回は、斜交座標をあまり使わない方法で解きますが、解き終わったあとに考察してみてください。
対称性を使え
つぎに、東大に限らず、遍く数学好きな人達が好むテーマが「対称性」です。
対称性には、
・文字の対称性
・図形の対称性
・確率の対称性
の3つを押さえましょう。
今回は、図形の問題ですが、文字の対称性に注目です。
点Aと点Bと点Cの順番を入れ替えたところで、何か違いが生じるでしょうか。全く生じませんね。これが文字の対称性です。
すると、答えも対称性のある図形になります。
先取りして、見てみましょう。これが答えの図です。
何となく、同じような図形が、3方向に並んでます。
これが分かれば、3方向のうち、1方向だけ調べればよいことになります。
点を打ちながら、面積を計算してみる
このあとは、色んなところに点Xを取ってみて、面積を計算してみてください。
そして、2から3に収まるところを考えていくと、何となく図形が見えてくることでしょう。
ここで、辺ABや辺BC、辺CAの延長線を超えたところで、点Xの動き方が変わることに気付けば、答えまであと少し。
いきなりここまでたどり着かないでしょうが、何度も試してみてください。
さて、前置きが長くなってますが、この問題は前置きに時間がかかる問題です。
問題の背景やカラクリを解き明かすまでは答案が書き始められませんが、解き明かしたらスラスラ進むのです。
(理系第3問は逆で、見た瞬間から計算し始められる問題ですね)
面積が等しい部分は、等積変形が出る。
このあとは領域を6分割して、面積を計算します。
すると、点Xを頂点に持つ三角形の面積が同じになるように、動かすことになります。
これを、等積変形と言います。
三角形の等積変形の基本は、平行線です。
今回は、点Xだけが動いて、底辺は動きません。なので、平行線によって等積変形できる超基本パターンです。
これに気付けば、あとは答えは簡単。
手書きの解答をどうぞ。
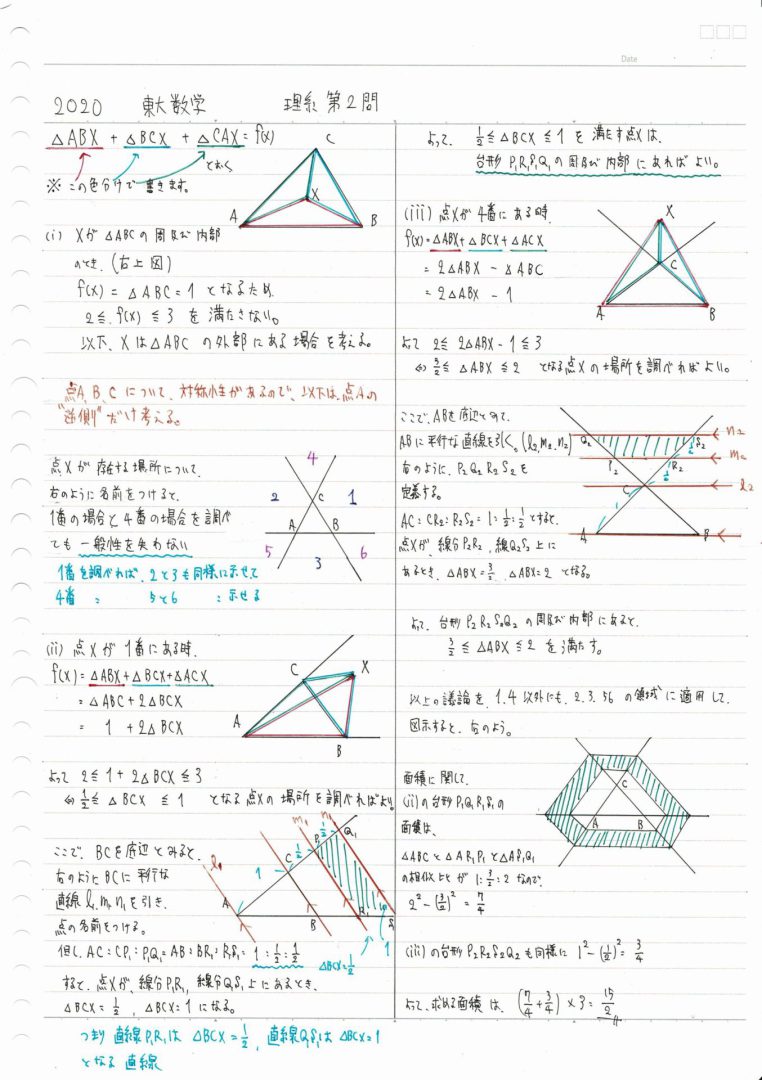
平行線が鍵!
このブログで、平面幾何について触れることが少ない(つまり、東大入試で平面幾何があまり登場しない)ので、折角だからあと少しだけ書いておきましょう。
平面幾何において、平行線が鍵になることがよくあります。
なぜなら、平行線の性質
①同位角や錯覚が等しい
②平行線の距離が一定
という性質が便利だからです。
①の「同位角や錯覚が等しい」に関しては、要するに同じ角度がたくさん出るくらいに捉えてください。
同じ角度が登場すると、何が起こるでしょう。
最も大切なのは、相似形が出ることです。中3で相似条件に「2角が等しい」があったはずです。
また、相似形からは、相似比や面積比、線分比が導き出されます。
円が絡むと、方べきの定理も導けます。
というように、一本の平行線で、あれやこれやと、色々な図形の性質が導ける可能性が広がるのです。
②の「平行線の距離が一定」に関しては、主に等積変形が対応しますね。今回はこれを使いました。
以上、簡単ではありましたが、平面幾何のポイントです。センター数学(もう終わってしまいましたが)に使える重要な考え方でした。
敬天塾作成の解説
2020(2)理数 解説こちらのpdfファイルは無料でダウンロードいただけます。
受験生の学習はもちろん、先生方の授業にお役に立てるのであれば、どうぞご自由にお使いください。
断りなしに授業時にコピペして生徒に配布するなども許可していますが、その際「敬天塾の答案である」ということを必ず明記していただくようお願いします。
ただし、無断で転売することは禁止しております。何卒ご了承ください。





