2020年東大理系数学（第1問）入試問題の解答（答案例）・解説

２０２０年　東大数学　理系第１問

数学は論理的ではない。

この問題を見た時思いました。「ついに東大でも、論理メインの問題が出たか！」

数学は論理の学問だと言われます。
しかし、それは違います。高校数学は論理的ではありません。
昔から批判していますが、高校数学までのカリキュラムは、主に微積分をマスターすることが目標に置かれているため、その他の分野の重みが相対的に軽くなっています。
端的に言えば「計算できるヤツが強い科目」なのが、今の高校数学です。

これには功罪ありますが、計算分野に重きが置かれてい過ぎるため、大事な「論理」の考え方が曖昧になっています。
教科書も参考書も問題集の解説も、よく読むと論理的に怪しいところが満載。

この部分を指摘する数学の先生も非常に多いです。

論理的に場合分けを学ぼう

例を挙げると枚挙に暇がないのですが、例えば「場合分け」。
本当はキチっと論理学を教えないと分からないはずの論理展開を、ごまかしながら教えられているのが分かるでしょう。

例題として、
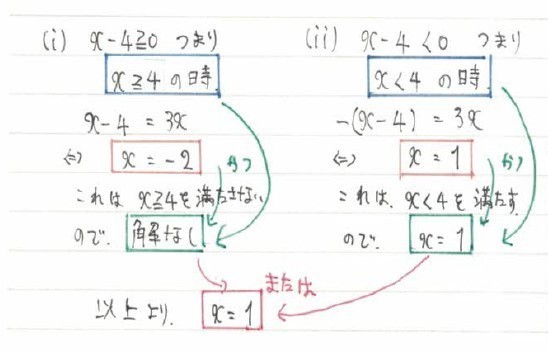
｜ｘ－４｜＝３ｘ　という、絶対値の方程式を解いてみてください。

さて、答えを出すことは簡単だと思いますが、論理展開を正しく追っているでしょうか？
あ、場合分けで解いてくださいね。「グラフで考えたほうが簡単だぜ」みたいなのは、今は本筋ではありませんよ。

さて、これを論理的に解くと、こうなります。

　｜ｘ－４｜＝３ｘ
⇔「ｘ－４≧０　かつ　ｘ－４＝３ｘ」または「ｘ－４＜０　かつ　ｘ－４＝３ｘ」
⇔「解なし」または「ｘ＝１」
⇔ｘ＝１

恐らく、１行目から２行目に行くときの論理展開を知らない人が多かったことと思います。

これを、ビジュアル化するとこうなり、

一般化すると、こうなります。

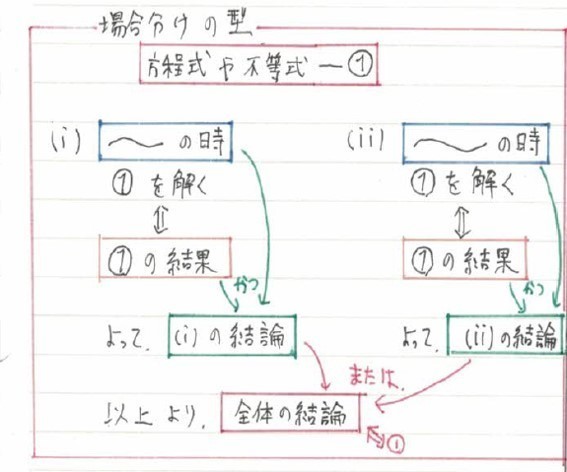
何気なく行っている場合わけも、論理的に捉えると見え方が変わると思います。
実は、こういうのが高校数学であらゆるところで存在しているのです。

論理に強くなる方法

東大の問題の解説からは脱線しますが、ぜひ１年後に東大を受験する皆さんであれば、論理に強くなってほしいと思います。

その方法は、一番確実なのは、大学数学レベルの論理の分野を学ぶのが良いのでしょうが、実際はかなり難しいでしょう。
なので、受験生レベルでできることとしては、「式変形をするときに、イチイチ必要性や十分性を考える」というのが現実的だと思います。

詳しく書くと大変なので、今回はここまでにしておきます。

第１問の難易度は、難しい？簡単？

さて、東大入試が解禁されると、難しかったか簡単だったかが話題になりますが、この問題の難易度はいかがでしたでしょうか？

高１でも解けるとか、簡単だとか、色々言われているのを拝見しましたが、私の評価は、世間の皆さんよりも「難しい」です。
なぜなら、上述した通り、論理展開を正しく追っていないと、しっかりと記述して答えられないだろうと思うからです。

大した計算がでないのは事実ですが、本当に自分の答案で、論理的に矛盾がないかを確かめられる受験生は、そう多くはありません。
邪推でしょうが、東大から「もっと論理的に数学を学べ」というメッセージとすら読めてしまう。

私は、この意味で新傾向の問題なのではないかと思いますので、来年以降も論理の話題はマークしておこうと思います。

（１）を解くカギは、普段の会話にあった

つい先日、妻とこんな会話をしていました。

平井「女性って、みんな甘いもの好きだよね。」
嫁「え？そうかな。甘いも嫌いって人もいるけど。」

別に、この会話は何も面白くはありません。そう、全く面白くないほど、どこにでもあり触れた会話だと思います。

しかし、これがこの問題の解説になっているの、気付きました？

問題文は、「ａ、ｂ、ｃはすべて０以上であることを示せ。」です。
これに対し、背理法を用い、「ａ、ｂ、ｃの中には負の数がある」と仮定すると説けます。

そうです。
「全て〇〇だ。」と言われたときに、例外を検討するのです。

先ほどの会話でも、女性の中で甘いものが嫌いな人をすぐに探しましたが、数学が得意だったり、論理的な考えをする人は、そういう考えのクセがあるのだと思います。

その後、（１）では、とても大きなｘを想定するのですが、極限を使うと便利でした。他にも解法がありますが、皆さんに勉強してほしいという意味で、極限を使う解法を載せておきました。

ちなみに、例外を探すコツは、極端な数を検討することです。
すごく大きい（＋∞の極限）や、すごく小さい（－∞の極限）、０や１、逆数や逆符号など、特殊そうな数から試していくと、例外が見つかります。

（２）「少なくとも」には背理法を使え

（２）も冒頭から背理法を使います。
これは、高校数学でよく習う、「少なくとも」を見たら、背理法を使え、の通りです。
今度は、とても小さなｘを想定するのですが、理屈としては（１）と同様なので、手書きの解答をご覧ください。

（３）「一般性を失わない」で手間を省け

最後、ｐ＝０を求めます。
これは、（１）と（２）の誘導にのり、ａ、ｂ、ｃのうち、０になる数を決めると筆が進みます。

途中で「一般性を失わない」という便利ワードがありますが、使いこなせてますか？ぜひ使えるように、身につけてください。

では、またドンドン更新していきます。お楽しみに。

東大受験に興味がある方は、敬天塾に関するこちらもご覧ください。
　　↓

◆日本一徹底して東大対策を行う塾　東大合格「敬天塾」
◇東大受験生のための図書館「知恵の館」
東大受験の貴重な情報を発信しています！

　↓　約１分の紹介動画です。