2021年東大文系数学（第1問）入試問題の解答（答案例）・解説

２０２０年東大数学　文系第１問

関数がｘ軸に接する条件

毎年出る３次関数の問題ですね。
条件１は簡単。ｘ軸に接する条件はアルアルです。

と言いつつも、意外とちゃんと説明されないと思いますので、ここで整理しておきましょう。
関数がｘ軸に接する条件というのは、「極値が０」です。基本的にはこれしかありません。極大値でも極小値でも構いません。
だから、今回の問題では、増減表を描いて、極大値＝０と極小値＝０を立式すればＯＫです。
ちなみに、ｙ＝ｘ＾３とｘ軸の関係のように、クロスしている時でも接していると言います。（つまり、この時ｘ軸はｙ＝ｘ＾３の接線です。こういう、細かい知識が大切。）

さて、これが２次関数になると話が少し複雑になります。
というのも、２次関数の場合は、極値を求める方法が微分だけではないからです。すなわち「平方完成」でも求められます。

また、２次関数とｘ軸の交点を求めるときに、連立して（２次方程式）＝０とできます。
２次方程式には解の公式があります。すると解の公式を利用した判別式も使える。
すると、（判別式）＝０の条件も使えます。

まとめると、
グラフがｘ軸に接する条件は
３次関数では、極値＝０のみ
２次関数では、極値＝０以外に、平方完成後のｙ座標＝０と、（判別式）＝０の３つ
が使えるということになります。

※細かい事を補足しておきます。受験生レベルでは知らなくて良い話です。
３次関数でも解の公式や判別式があります。
しかし、３次方程式の解の公式（カルダノの公式）は事実上使い物にならないほど複雑ですし、３次方程式の判別式も使いづらい。ということで、普通は使いません。

見慣れない問題にどう対処するか

これを使うと、ｂ＝４ａ＾３という式が得られます。(詳しくは手書きの解答をご覧ください。）
これで、文字定数が一つ減り、あとはａだけになりました。
ここから、条件２を使います。

条件２は、「指定された領域に格子点が一つだけ含まれる」という見慣れない条件。
問題文には「ｘ座標とｙ座標がともに整数である点」と書かれていますが、これは教科書に格子点が登場しない事実から来る、受験生への配慮であって、普通「格子点」といいます。
それに、格子点の問題は問題集などに平気で登場しますから、多くの受験生が知っていたことでしょう。

さて、この条件２。上には「見慣れない」と書きましたが、その通り。誰も見たことがない条件です。
このような時どうするかというと、過去に解いた同じような問題を思い出すしかありません。

とりあえず図を描いてみると、

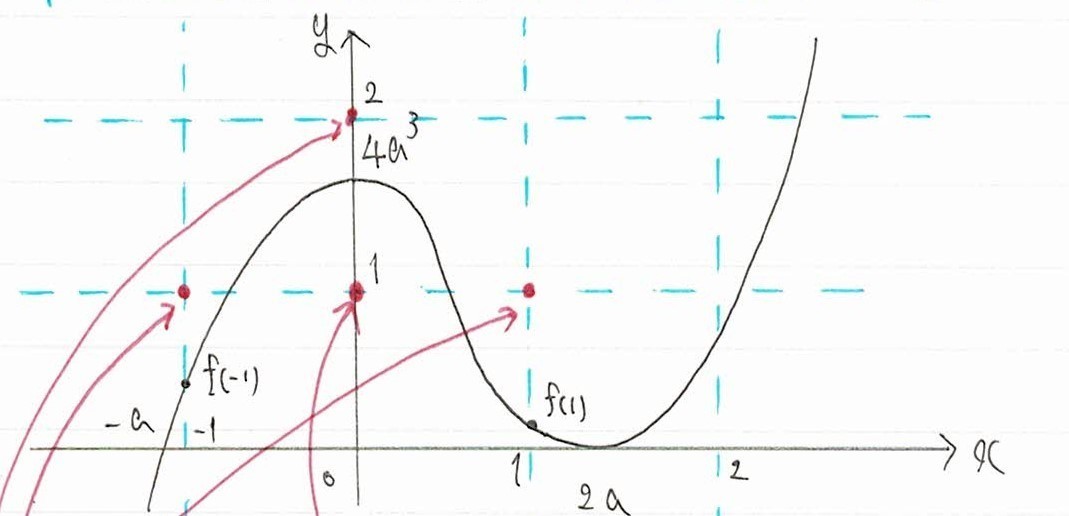
こんな感じになればよいと分かります。
すると、（０，１）は領域内に含まれて、隣の点は領域外になればよいと分かります。
これは、グラフが通る場所を特定する話ですから、いわゆる解の配置の問題です。
これを応用すると、解ける問題でした。

では手書きの解答をどうぞ。

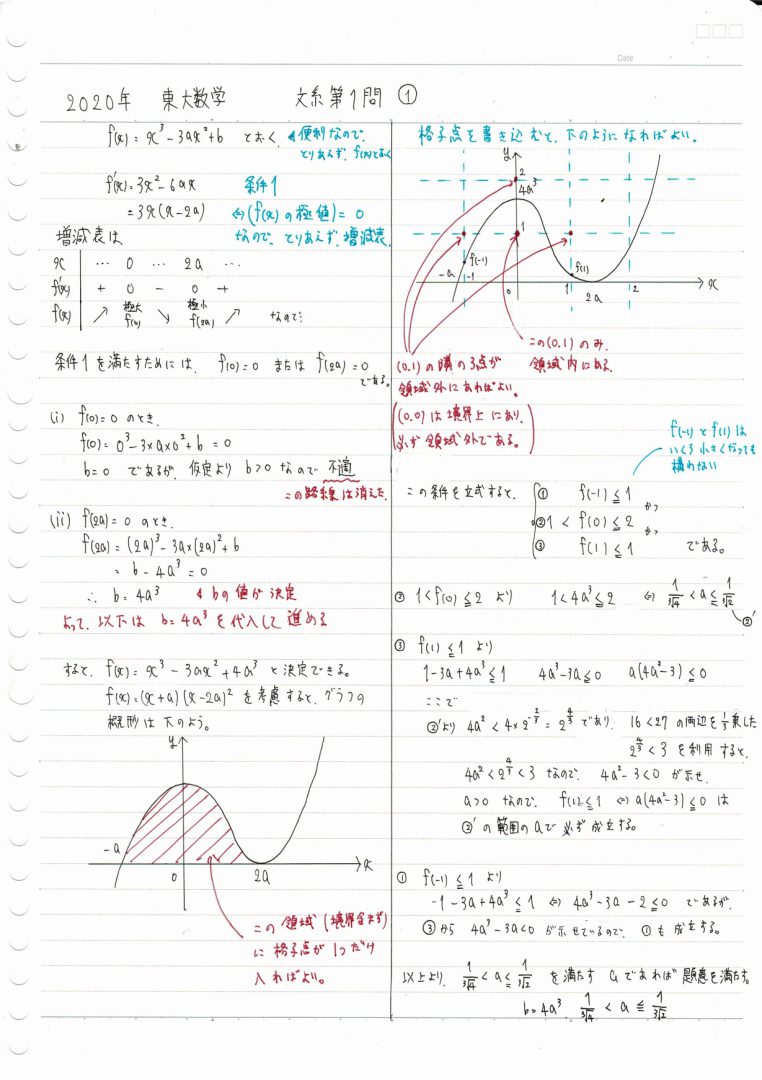
なお、条件２の立式は、少しだけ違う式にすると簡単に不等式が解けるのですが、今回は、発想の簡単さや、見た目を整えることを優先してあります。

全体

難易度としては、例年の東大入試の問題と同じくらいかなと思います。簡単でも、難しくもない。
ただ、格子点を領域内に含む条件を、自分で考えて立式するところは、焦っているとミスしやすいような気がしますね。
初見の条件を、自分で考えて立式するものは、過去にも何度も出題されているタイプです。なかなか身につかない能力かもしれませんが、訓練によって身につけられますんで、演習に取り組んでほしいと思います。

敬天塾作成の解説

こちらのｐｄｆファイルは無料でダウンロードいただけます。
受験生の学習はもちろん、先生方の授業にお役に立てるのであれば、どうぞご自由にお使いください。
断りなしに授業時にコピペして生徒に配布するなども許可していますが、その際「敬天塾の答案である」ということを必ず明記していただくようお願いします。
ただし、無断で転売することは禁止しております。何卒ご了承ください。