数学７月②「整数」

こんにちは、スタッフAです！
今回から、「整数」を扱います。
まずは、授業で学んだことを整理しました。

離散数：簡単に言うと、すきまのある数　例）自然数、整数など
連続数：簡単に言うと、すきまのない数　例）実数、有理数など
この２つは、概念が全く異なり、２つの間には越えられない壁がある。なお、整数の分野では「離散数」の考え方を用いる。

東大は、ユークリッドの互除法に関する問題を出題することがある。
東大は教科書で整数の分野が扱われる前から、整数の問題を出題していた。当時は対策が難しかったが、教科書で整数が扱われるようになった現在は、主に教科書の範囲で出題されるため、対策がやや容易になった。

「整数」
1、候補の絞り込み方
整数問題は、候補を有限個に絞った時点で、事実上の勝利。
1 不等式で挟む(すると、候補が有限個になる)
2 積=整数 の形に持ち込む（これでも、候補が有限個になる）
の2つが大きな方針。

2、不定方程式
積=整数 に持ち込む。
AB=整数 となった場合、AとBの大小や符号を調べる。(大小比較は、不等式の証明を思い出す。)

3、素数の扱い
素数　1とそれ自身しか約数を持たない自然数のこと。
AB=素数 のときは、片方が±1
（例えばエラトステネスの篩から）5以上の素数は全て、6k±1と表せる。

4、ユークリッドの互除法について
最大公約数(GCM)を求める方法。
GCM=1の時、互いに素。
文字式のGCMや互いに素は、ユークリッドの互除法
ｘとyの一次方程式を満たす（x,y）の整数解は、ユークリッドの互除法

5、最大公約数(GCM)と、最小公倍数(LCM)
a=a′g
b=b′g
l=a′b′g
ab=gl
a′とb′は互いに素

この、4式1条件を立式して計算する。

6、その他覚えたいこと
隣り合う2整数は互いに素
隣り合う2奇数は互いに素
aとbが互いに素なら、a+bとabも互いに素
5以上の素数は全て、6k±1と書ける(エラトステネスの篩)

今回は、とくに重要な問題を１問共有します。

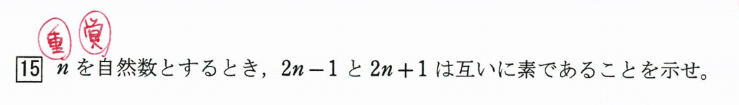
以下、解答。

次回も、整数を扱います。