数学8月②漸化式
こんにちは、スタッフAです!
今回も、漸化式です。
授業で学んだことをまとめました。
偶奇の問題は、偶数と奇数で異なる数列が現れる。
2コずれでも、特性方程式の書き方は変わらない。
偶奇に関する問題は貴重。見つけたら積極的に解こう。
↓これは、偶奇で数列の定義が変わるという変わった問題。


復習
「互いに素」であるか示す→背理法や対偶命題
「互いに素」=G.C.M が1→4式1条件 a=a^’ g
b=b^’ g
l=a^’ b^’ g
ab=gl
aとbは互いに素
その他の漸化式のパターン
・階差を取ると、「微分」のように次数が下がるので、定数項がついていても、階差をとればなくなってしまう。
・漸化式と余りが絡んだ場合は、周期を探ること!
・漸化式とユークリッドの互除法が、相性が良い。同じ理由で、帰納法とも相性が良い。
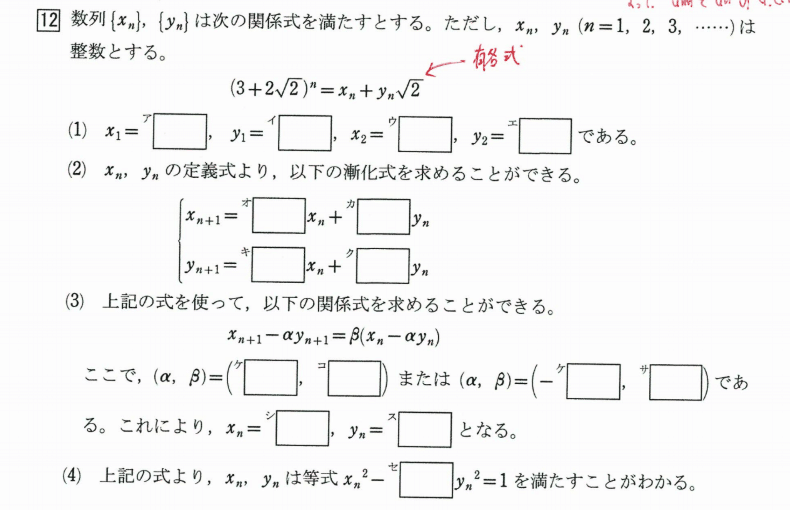
授業の後半では、有名な方程式 ペル方程式に関わる周辺問題 (3+2√2)^n=x_n+y_n √2 を扱いました。
ペル方程式は
・無理数のn乗を漸化式で表現。面白い性質が多数。
・二種混合の連立漸化式が登場
・共役な無理数でも、同じ漸化式が登場。
・和を取ると、整数になる。
・2次方程式の解のn乗の和は、係数が同じの3項間漸化式になる。
ペル方程式に関する問題も紹介します。
解答



次回は、確率漸化式です!



