数学９月②「ベクトル　斜行座標の導入」

こんにちは、スタッフAです。
今回は、「ベクトル　斜行座標の導入」です。
斜行座標は、答案に書くわけではないけれど、理解すると問題が解きやすくなる捉え方です。
基準となるベクトル何個分なのか考える必要があります。

この問題では、答案の図を、赤い手書きの図のように、右下にAを置き、座標上で考えます。

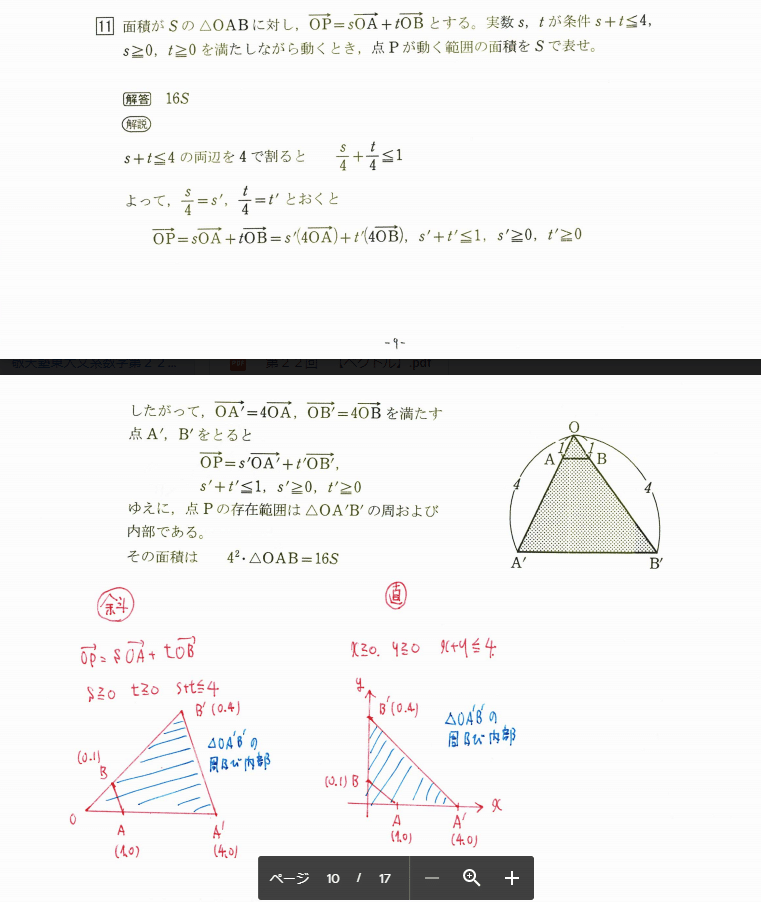
この問題では、斜行座標の条件を直交座標に直して図示し、それをまた斜行座標に戻して考えます。
授業で使ったレジュメの一部を紹介します。

1、斜交座標の導入
・大学受験において、ベクトルの意義は「斜交座標」が導入できること。
・OAベクトルが(1,0)、OBベクトルが(0,1)に対応すると考える。
・高校ベクトルで登場するのは、内分、外分、直線の傾き、直線の交点、存在領域くらい。

3、チェバの定理、メネラウスの定理、天秤
・しかし、天秤の方法を覚えると、チェバもメネラウスもほぼ不要。

5、基底の変換
・基底のベクトルとは、(1,0)と(0,1)になるベクトルのこと。
・斜交座標は、基底のベクトルを変換することで、軸の向き(や長さ)が変えられる。

今回習った天秤を使えば、線分の比を求めるのがとてつもなく簡単になります。いままで、チェバとメネラウスを思い出しながら解いていた問題も、天秤の使い方さえ覚えておけば安心です。

次回は「図形総合　三角比」です。