数学９月③三角比

こんにちは、スタッフです。
今回扱う三角比はとても浅い単元で、正弦定理、余弦定理、面積=１/２a・b・sinθ、面積＝（a+b+c）・ｒ/２、ヘロンの公式が使えれば良いそうです。

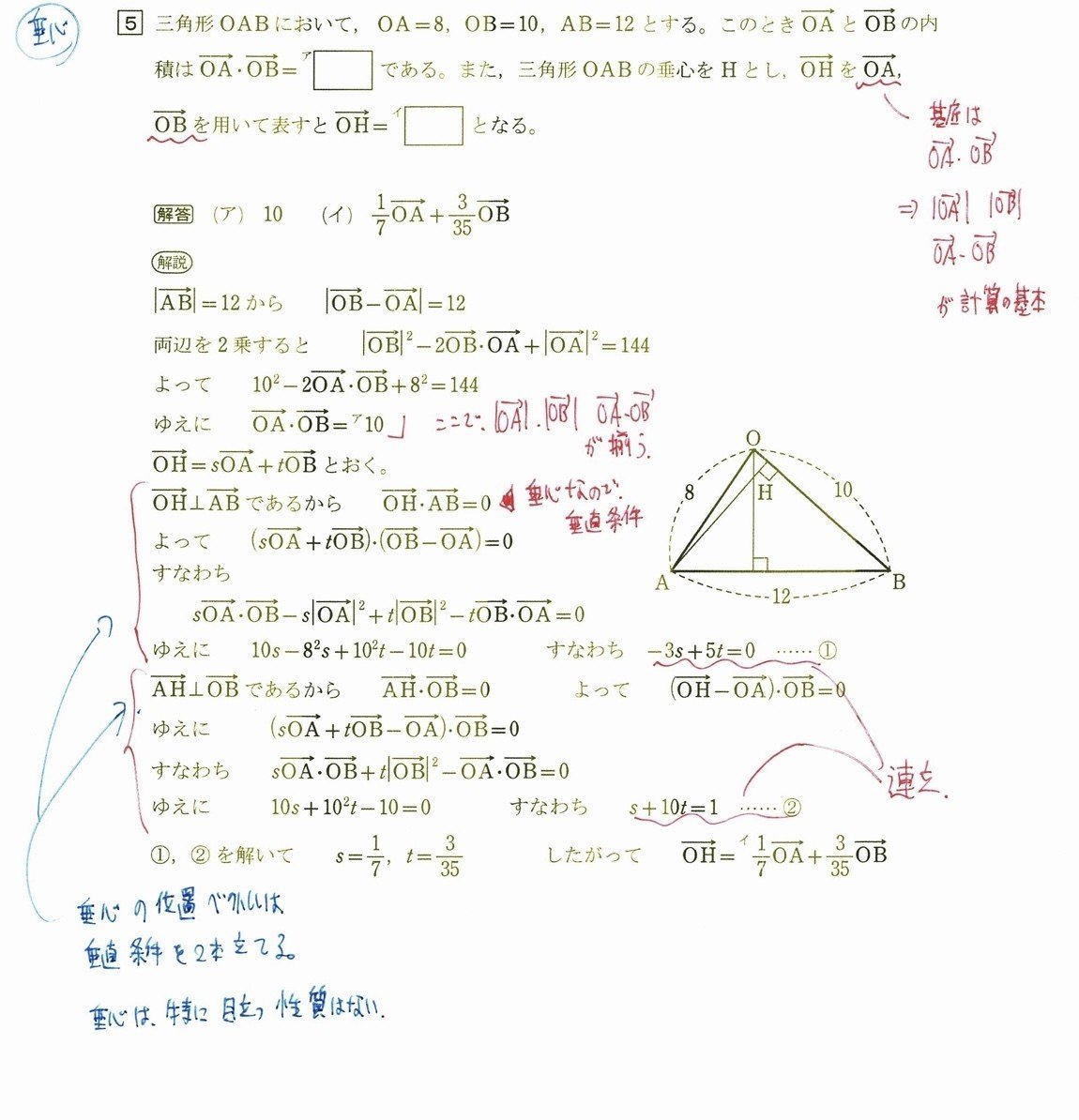
垂心は特徴がありません。この問題では、垂直条件より、ベクトル・ベクトル＝０を２本立てて、連立して解いています。
OHをOAとOBの実数倍で表す問題は頻出ですね。
（アルファベットの上に矢印があると思って見てください）

メモ　天秤、角の二等分線の定理、メラネウス、チェバなど千分比のルーツはすべて相似である。

１本めの赤い波線のところ、｜AP｜cos∠PABはわかりません。でも、垂直二等分線上にあることはわかっているので、＝AMになります。だから｜AB｜｜AM｜と表すことができます。

（４）の面積の公式は、まだ覚えていなかったので、載せておきます。

３辺が分かっています。合同条件と同じなので、三角形の角度も分かると気づくでしょうか。

直角が登場する問題は、座標を導入しましょう。むしろ、図形の問題には、常に座標の導入を検討しましょう。

（３）９０°だ！
三平方、ｍ_１×ｍ_２＝－１、内積＝０のどれを使うのか、脳内でググれるようにしましょう。
また、分母に文字が来たら、０の可能性があるので場合分けが必要です。「面倒だ」とすぐに気づけるようにしましょう。

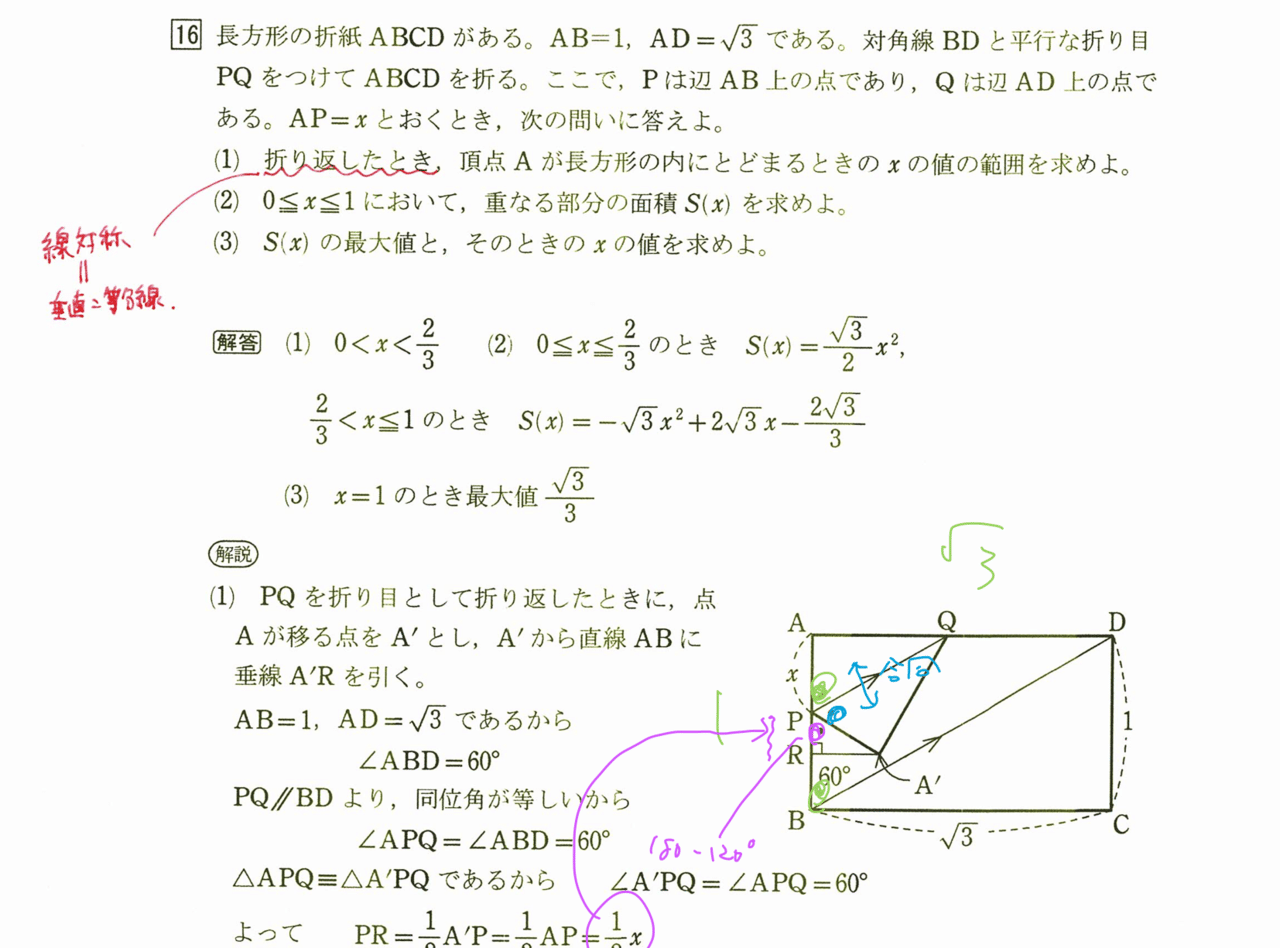
折り紙の問題は、線対称＝垂直＝垂直二等分線を用いると気づけるとよいです。

次回は、空間図形です！