数学6月②分数関数と領域図示

こんにちは、スタッフBです。

今回は、分数関数と領域図示です。

分数関数を＝aと置いて、実数解の条件でxを求めていく。

xとyの同次式は1変数にする。

具体的には、「y²で割る」や「予選決勝法」。

予選決勝法は

2次関数なら判別式から実数解の条件やはじきを求めていく。

3次関数なら、固定して微分。

同次式。y²などで割って、x/yを＝kで置換している。

1次方程式の解の配置の問題は貴重である。

なお、東大入試2015年第2問に登場する。

図形の問題で問われることは3つ。

長さ、角度、面積。

よって、図形の問題が出てきたら、どれかを文字で置くことになる。ただし、面積を文字で置くことはほぼない。

図形に関数が絡む問題は、難度が不明。警戒が必要。上記3択を忘れないように。

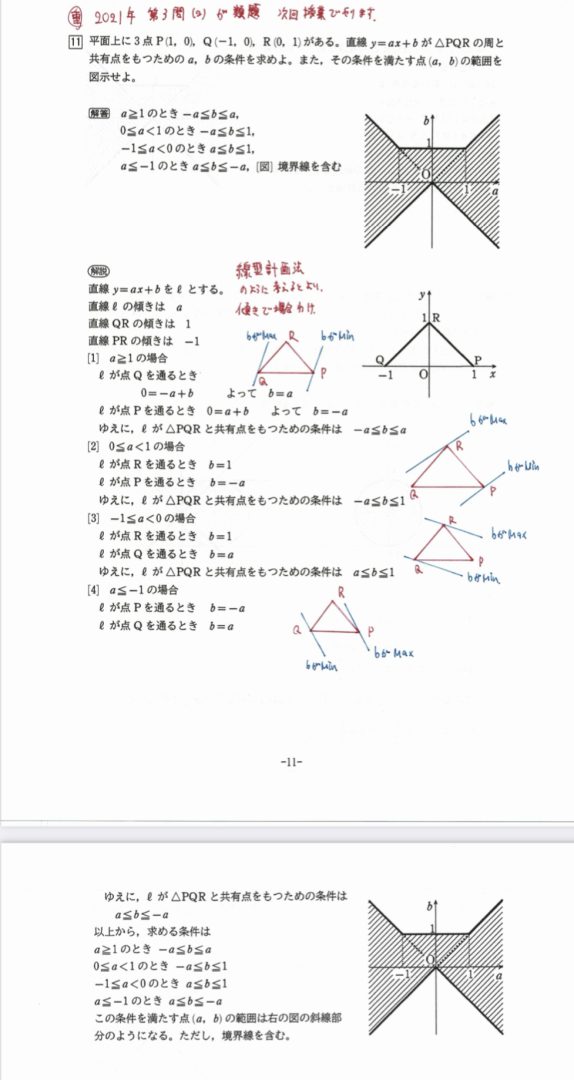
東大入試2021年と類似。

直線と三角形の共有点を求める問題。

2018年第1問

ルート＋ルートの最大最小はやっていないはず。何か変だと感じること。

（1）は計算はややこしいが、理屈は平易な問題。

（2）「すべて」の使い方が珍しい。

Dの領域が不等式の領域に含まれることを読み取れなかった受験生が多かったらしい。

場合分けを丁寧に行う問題。

25分使っても良い。数学は、すべての問題に手をつけるわけではないので、確実に正解できるのなら40分かけても良いかもしれない。

※

この問題は計算量が多い。記述量も多いので、答案に収まらない可能性がある。いかにシンプルに書くかが問われる。

領域図示の場合は、右側⅓程度を図示のスペースとして予め取っておくと良い。

1995年第1問

良問。同次式の問題。

2変数だ！→1変数にする→y/xを作る、予選決勝法で解くなどを検討。

y/x＝tと√y/x＝tのどちらがよいかは、途中まで計算しないとわからない。

tの2次式に持ち込み、2次の係数＞0、＜0、＝0で3つに場合分けして、＞0の場合のみがkの条件となる。