2022年 東京大学 数学　文系第4問

複雑な設定

こんなん問題文を読み解くだけで疲れる！
理解してしまえばシンプルな設定なんですが、理解するまで苦労します。

超簡単に説明しましょう。
「コインで裏が出たらくるっと１２０度回転させる。表が出たら長さ１だけ直進する。」
これだけです。僕は、頭の中で、ミニカーをクルクル回転させたり、直進させたりするイメージでとらえました。たったこれだけのことなんですが、数学で表現すると、問題文のように複雑になってしまいます。（憎し）
※問題文をそのまま読み取ると、表が出た時に裏の回数を読み取って直進するように書いてありますが、裏が出ても別にどこにも移動しないので、裏が出た時点で１２０度回転させておいてもＯＫです。

これだけ簡潔に理解できれば、だいぶ簡単なんですが、ここまでが難しい。
しかも、これを説明するのには、（１）を解きながら具体的にコインの出方によって実験するしかないというのが苦しいところ。

どうでしょうか？ご理解いただけましたでしょうか？

（１）実験しよう！

要約すると、５回コインを投げて、ミニカーが原点に戻ってくればよいです。

ということは、全部裏が出ることで、原点でクルクルするだけの場合か、「表裏表裏表」と出て、０度方向、１２０度方向、２４０度方向に１回ずつ進むかの２択です。

それぞれ計算して和を取ればOK。設定が理解できれば簡単です。

なお、（１）は複雑な問題文を簡潔に理解して、移動の仕方を捉えるために、実験させる設問です。問題文の意味が分からなければ、コインを頭の中で投げてみてどういう動きをするか考えてみるしかありません！

（２）突然の重複組み合わせに気づけるか？

本丸の（２）。
９０回表、８回裏を出し、ミニカーが原点に戻って来る確率を求めよとな。
裏が８回だから、クルクル１２０度回転させる回数も８回です。ということは、回転方向でいうと、２回転半くらいですね。

裏と裏の間に表が挟まって直進するため、何回目の裏と裏の間に表があるかを数えなければなりません。
イメージ図でいうと、こんな感じ。（〇が表で、×が裏）

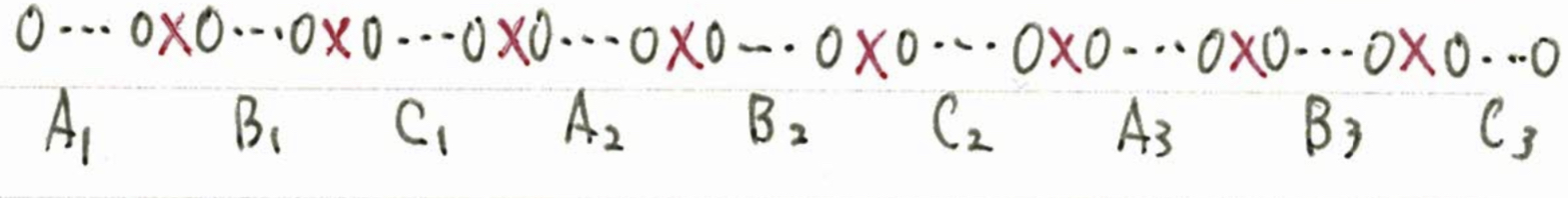
A1とA2とA3が０度方向に進む場所で、B1とB２とB3が１２０度方向、C1とC２とC3が２４０度方向に進む場所です。

裏（×）の場所はある程度移動しても良いのですが、大事なのはA１とA2とA３の合計数。
原点に戻って来なければならないので、０度方向と１２０度方向と２４０度方向に、それぞれ３０回ずつ直進しなければなりません。
ということは、A1とA2とA3の場所にある表の合計数が３０個。同様に、Bの場所もCの場所も合計３０個ずつです。

こいつを重複組み合わせで計算して終わりです。

まとめ

この問題の難しいところは、まずは設定を解釈、理解するところ。複雑なので何度も実験して確かめましょう。
そして、９８個の順列です。〇と×がこんなにたくさん登場する場合の数は、初めてだった方も多いことでしょう。重複組み合わせが突然登場するところも不慣れかもしれません。

よ～～～く、ゆ～～くり試せば理解できるのでしょうが、シンプルに捉えるまで時間がかかるし、難問でした。良いところ（１）だけ解いて終わりという受験生が多かったようです。

【さらに深く学びたい方のために】

敬天塾では、さらに深く学びたい方、本格的に東大対策をしたい方のために、映像授業や、補足資料などをご購入いただけます。
ご興味頂いたかたは、以下のリンクからどうぞご利用下さい。

映像授業【東大文系数学】

↑ まずは目次と無料部分だけでもどうぞ。