2018年東大理系数学(第3問)入試問題の解答(答案例)・解説(パラメータ、通過領域と軌跡、面積計算)
【関連ページ】東大文系で頻出の通過領域の解法パターンをすべて紹介した決定版(逆像法・順像法・包絡線・線形計画法など)
目次
2018年 東大理系数学 第3問の解説(パラメータの扱い方、通過領域と軌跡、面積計算)
文系の第4問と共通問題です。(難易度は大分違いますが)
理系第2問のときにも書きましたが、この年の共通問題は文理で難易度がかなり違います。ということで、両方を見比べて学ぶと非常に効果が高いように思えます。
(但し、文系がこの理系第3問を見ても、分からなくなっちゃいますが。)
領域(軌跡)の問題
では具体的に問題に行きましょう
今年は小問の数が減りました。この問題も小問構成ではなく、大きな一つの問題です。
問題の設定としては、動点が二つ(PとQ)が与えられ、さらに正の範囲で動くkが与えられます。この3つの文字と連動する点Rが通過する領域を求めるという、凝った問題です。
ちなみに、点の通過領域のことを「軌跡」と言います。
ということで、この問題は、「点Rの軌跡を求めよ」と言い換える事も出来なくはない・・・のですが、領域と言った方が分かりやすいと思います。
パラメータ多いよ!
点Pや点Qのパラメータの設定の仕方は、問題ないでしょう。
これをベクトルの成分として代入して、ORベクトルを作れば、点Rの座標がpとqとkを用いて表せる。恐らくここまでは、多くの受験生が到達したことと思います。
しかし、問題はここから。
通常はパラメータは一つ。せいぜい二つ登場する程度です。例えばこちら。
数研出版の教科書の例題ですが、円に連動する軌跡を求める時に、sとtの2文字を設定することも出来ますし、
角度をθとおいて、三角関数で軌跡を求めることも出来ます。
しかし、今回は3つ。
ここで、方針を見失ってしまう人も多いでしょう。
どう考えれば良いのでしょうか?
基本に立ち返ろう!
先ほども書いたとおり、この問題は「通過領域」の問題でもあり、「軌跡」の問題でもあります。
そしてパラメータ付の軌跡の問題は、パラメータを消去するのが鉄則。ということで、pとqとkのうち、どれから消去しようかな~?と考えます。
別の言い方をすれば、「文字が多い時は、消去せよ(減らせ)」。数学では非常にポピュラーな格言もありますね。
いずれにしろ、困った時は基本に立ち返ることが大事だと思います。
結論からたどれ!
また、結論からたどっても良いでしょう。求める面積の式をご覧ください。「S(k)を求めよ」となっています。
という事は、最後に求める式はkの式。よって、kを消去するのはNG。残さなければなりません。
では、qを消すのかというと、qは1か所にしか登場しておらず、代入することが出来ません。
ということは残ったpを消すのが自然な発想でしょう。
このような考えをして、pを消すという結論に至って構わないと思います。
kを動かすか、qを動かすか
pを消去すると、xとyの関係式が得られます。これが軌跡の式です。
しかし、まだkとqが残っています。
これをどう考えるかですが、先ほど上にも書いたとおり、kは最後まで残さなければならない文字です。
つまりkはこの時点で動かすべき文字ではありません。定数と見なして、qを動かすのがセオリーです。
ではqを動かすのですが、ラッキーなことが起こります。なんとqを動かすと、放物線が左右に(厳密にはx軸方向に)動くだけ!
まあ、そりゃそうです。点Qが、原点と(1,0)の間をウロウロする動点ですからね。
ということで、放物線を左右に動かす問題へとすり替わります。
場合分けを丁寧に。図を描きながら考えよう
そして、最後の砦。場合分けの登場です。
放物線が左右に移動するのは分かりましたが、左端と、右端でどこまで移動するかによって、求める図形のカタチが変わってしまいます。
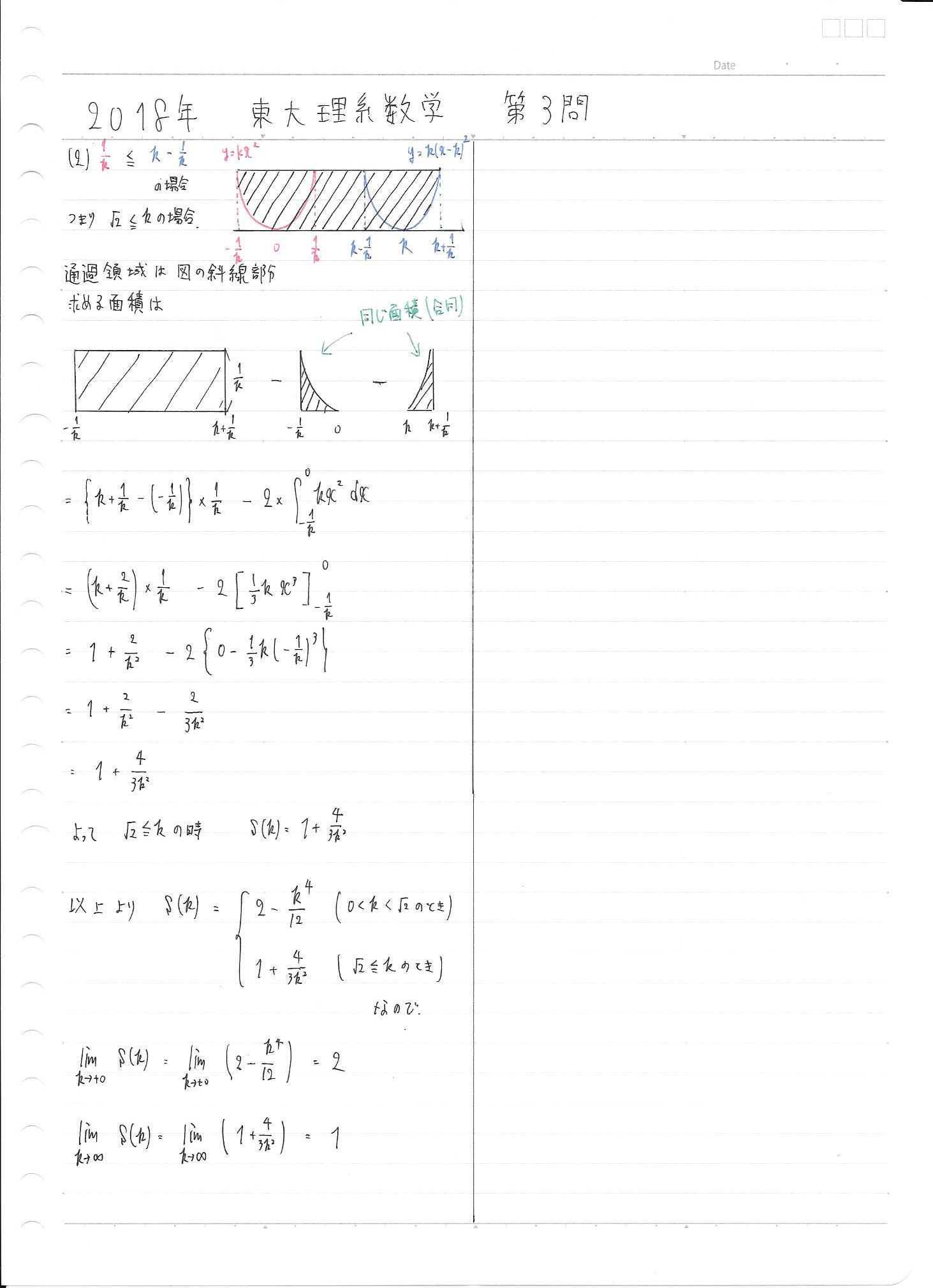
この場合分けが、いささか厄介なんですが、手書きの解答で詳しく書いておきましたので、どうぞご覧ください。
面積計算が面倒
放物線が、遠く離れない方(手書きの解答でいう、(ⅰ)の方)の面積計算が、面倒ですね。ここで計算ミスが多発しそうです。
東進も河合塾も、簡単な計算方法をネット上に掲載しています。どちらも同じ方法なので、キレイな方を選んで東進のものを載せておきます。
確かに、こんな見事な等積変形が、入試の会場で思いつけば良いのでしょうが、余程冷静であるか、普段からこのタイプの等積変形に慣れ親しんでいる人しか出来ないのでは?
そんなに頻繁に登場するものでもないし、どちらかというとセンターテクニックのような感じ。
恐らく、発想出来る人の方が少数派だと思うので、僕は手書きの解答に、素直に分割して計算する方法を書いておきました。
このブログでは、ウルトラCみたいな解答や、美しく、切れ味の鋭い解法よりも、「受験生にとって、試験会場で使いやすい解法」を心がけています。発想力よりも、積み重ねた努力の末に使いこなせる解法の方が、実用的だと思いますので、参考にして下さい。
最後の極限計算は、非常に簡単。問題ないと思うので、この問題の解説はここまでにします。