2019夏 河合東大オープン 文系数学第4問の解説(整数、互いに素、分数式が整数になる条件)
目次
2019年夏 河合東大オープン 文系数学第4問の解説
さて、第4問。
典型的な整数問題。
(2)も、かつての難しさほどではなく、東大受験する人ならば知っておきたい解法というレベル。
取りたいです。
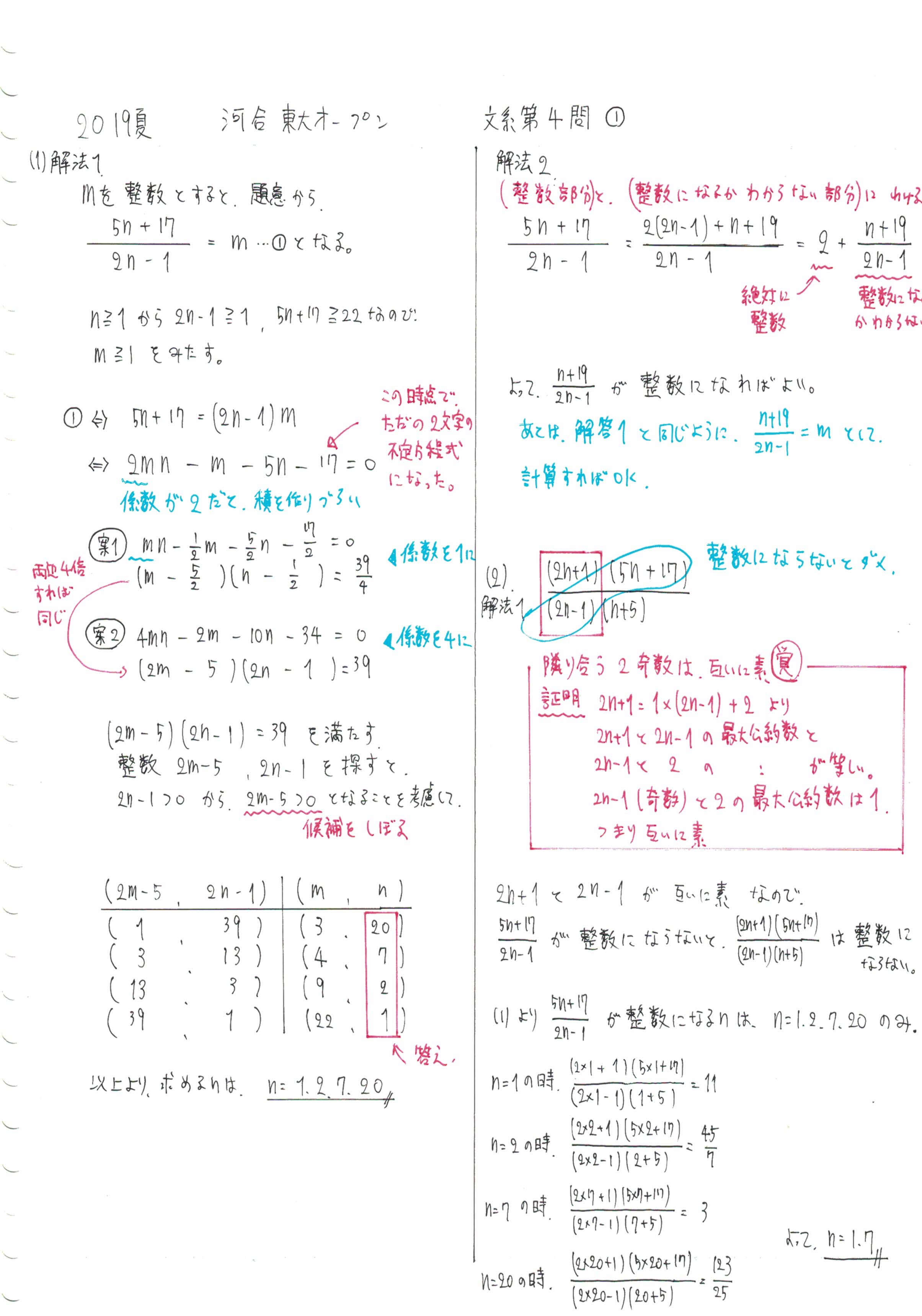
(1)何も難しいところはない。
では、(1)からいきますが、これは何も難しいところはありません。できなかった人は、反省するレベルでしょう。
与式が整数になると言われているので、「=m」かなんかでおき、分母を払うと不定方程式が出てくるというだけ。
どこにも不自然な発想がありません。
数弱の人は、
(東大模試だから、きっと難しい解法をするんだろう)
などという、余計な忖度をするかもしれませんが、むしろ逆。
誰でも知っている解法の積み重ねに答えがあるのです。
東大だからと言って、特別ではありません。
割り算をして次数を落としてもよい。
また、割り算をして次数を落としてもよいでしょう。
分子÷分母をすると、(整数部分)+(nの分数式)となり、後半の(nの分数式)の部分が整数になればよい、という論理です。
分数式は割って考えることがある
というのも基本。但しこの問題に関しては、割っても割らなくても、大した違いはありませんでした。
では(1)の部分だけご覧ください。
(2)発想は悪くないけど、解けない問題について
では、(2)へ。
同じようにnの分数式が与えられています。
もちろん、瞬殺で解法が思い付く人はいないでしょうから、アレコレ考えるわけですが、
(1)と同じように、「=m」とおいて、分母を払って解いてもOK。
結果として解けませんが、(中々面倒な式が出てきます)発想としては悪くありません。
ちょっと脱線しますが、こういう入試問題で、一つの方針を試した後に答えが出なかったとき
(自分の方針は間違ってたんだ。やっぱり数学が苦手なんだ。)
と思う人が多いのですが、実はあながちそういうわけでもありません。
スタンダードに考えたら採用するような解法が通じなかっただけで、発想自体は悪くないことが多いのです。
解けない方法は悪、解ける方法は善。
と単純に捉えるのではなく、「なぜスタンダードな解法では解けなかったのか」と考えるべきでしょう。
どのように(1)を利用するか
ということで、(1)と同じ解法を試して挫折したとき、どうするのか。
やはり、(1)からの誘導を見るべきでしょう。
(というか、ぱっと見で気付く人も多いでしょう。)
「数学の問題は全て誘導問題だ!」と決めつけて解くのが定石ですから、散々いろいろと試した後に「ああ!!誘導だったのか」と気付いてはいけません。
よく見ると、(1)で求めた式が一部に登場しています。
(あ、なるほど、ということは(1)の結果を利用するんだな)と思い、その路線で試行錯誤を始めましょう。
ここで大事になるのが、次のセクションの事実です。
隣り合う整数は互いに素、隣り合う奇数は互いに素
ご存じでしょうか?
①隣り合う整数は互いに素
②隣り合う奇数は互いに素
という、有名事実があります。
①の方が有名ですが、②も一緒に覚えておきましょう。
(ちなみに、隣り合う偶数は、互いに素になりませんよ。どちらも2の倍数ですから)
①の証明ですが、
n+1をnで割ると、
n+1=n×1+1
となりますね。
ユークリッドの互除法としてみると、
n+1とnの最大公約数が、nと1の最大公約数に一致しています。
nと1の最大公約数は1ですから、n+1とnの最大公約数も1。つまり、互いに素なのです。
(最大公約数が1になることを互いに素と言います。)
これとほぼ同様にすると、②も証明できます。
手書きの解答に書いておいたので、必ず確認しておいてください。
分数式が整数になるには、分母を割り切らなくてはならない
では、最後。
分数式が整数になる問題のアプローチとして、重要なことですが、
分数式が整数になるには、分母を割り切らなくてはならない
というのを解説します。
分数に見えるのに、全体として整数になるということは、分子÷分母が割り切れてしまい、分母が消えてしまうということです。
そして、分母の(2n-1)に注目すると、分子の(2n+1)か、(5n+17)に割ってもらわなければならないのですが、
先ほどやった通り、(2n+1)と(2n-1)は互いに素ですから、割り算が出来ません。
ということで、(5n+17)/(2n-1) (つまり(1)の部分)が割り切れなくてはならなくなります。
すると、候補のnは(1)で求めた4つ(1、2、7、20)だけになり、あとは試せばOKということになります。
この論法は、整数問題で非常に重要。よく見る流れですので、必ず押さえたいものです。
では、手書きの解答をお見せしましょう。
別解の紹介 割り算したら?
おまけで別解の紹介です。数学で高得点を取りたい場合、必ず別解の検討をしてください。
というか、別解の検討を必ず行い、解法の体系化が出来たら、ほとんど大学受験の数学の勉強は終わりと言ってよいでしょう(どこでも受かるレベルになれます)
まずは、(1)と同じように、分数式を割った場合ですが、やはり解けます。考え方も、そんなに変なところはありません。
ただし、(整数部分)+(nの分数式)となるのですが、分母がnの2次式なので、(1)と同様にいきませんから、nの候補を絞る作戦に出なければならないのが、少し難しいかもしれませんね。
数Ⅲの極限の話を知っていると、この辺りが発想しやすいんですが。
別解の紹介 どうせ5くらいになるでしょ?
この記事、理系の受験生ってみてるんでしょうか?
東大理系の受験生って、あまり文系の問題まで手を出さないような気がするんですが、あれなぜでしょう?
めちゃくちゃ勉強になるし、同じ人が作ってるんだから、明らかに分析の対象だと思うのですが・・・。
ということで、理系的に発想した解法も載せておきます。
与式って、発散すると5に収束しますよね。
ということは、nが大きくなればなるほど、5にちかづく。
ということは、ほとんどのnを代入しても、5付近の値になってしまうのです。
ということで、
①5にならないnを探す
②5になるnを探す
の2通りを検討すればよい、という発想です。
似たような発想の問題が、2018年に出題されていますので、これもチェック!
では、河合文系はこれでおしまいです。