2020年東大文系数学（第3問）入試問題の解答（答案例）・解説

２０２０年東大数学　文系第３問

今年の中で、２番目に取りやすかった問題でしょうね。
第１問と、これが解けて他は取れなかったという人も多くいるはず。
見ていきましょう。

通過領域の解法は３つ

さて、まず登場したのは通過領域の問題。
通過領域は、東大文系で何度も出題されている頻出かつ、絶対に出来るようにしなければならないテーマ。
しっかり解法を確認していきましょう。

まず、知らなければならないのは、解法が３つあるということです。
（ブログでも、何度も書いている気がします。）
①パラメータの解の配置
②ファクシミリ論法
③包絡線
の３つです。

そして、参考書や問題集の解説で、３つとも紹介されることは少なく、紹介されたとしても名前がついていないため、読み手が混乱に混乱を重ねてしまうのが、最大の障壁です。
先生が良かれと思って、一つの解法しか紹介しないこともありますが、それがかえって参考書を読みづらくしてしまうこともあるため、一つずつきちんと理解しなければなりません。

詳しくは手書きの解答に任せるとして、簡単にだけ触れておきます。

①パラメータの解の配置に関しては、まず通過する曲線（直線）を立式し、（ｘとｙではない）パラメータで降べきの順に並べます。
そして、そのパラメータが与えられた定義域に解を持つ条件を立てる、という流れです。
メリットは、解の配置の解法自体は誰でも習うので使いやすいことで、デメリットとしては計算量が（他のものに比べて）多くなることが多いということでしょう。

②ファクシミリ論法は、①と同様に通過する曲線（直線）を立式した後、ｙ＝（ｘとパラメータの式）の形にします。
次に、右辺についてｘを固定し、パラメータの関数と見なします。そして右辺の取りうる値（最大値や最小値）を求めるという流れです。
メリットは、①より計算量が少ないことが多いことと、デメリットは新たに解法を覚えなければならないことでしょう。

③包絡線は、元の直線の式と、パラメータで微分した式を連立すると、常に接する曲線が求められるというものです。
メリットは、使えると一番計算量が少なく簡単に答えが出る場合があることで、デメリットは、通用しない問題があることでしょう。他にも、計算方法が覚えられたとしても、なぜこの計算（パラメータで微分して連立）で求められるかが分からないため、わすれやすいようです。

（１）は上のどれでもなく、図形的なアプロ―チで解いてよい？

さて、（１）は通過領域なので、上の３つのどれで解こうかと思うわけですが、上のどれでもない解法でも良いかもしれません。
というのも、いくつか理由があります。

①半直線ＯＰと設定されていたり、放物線Ｃがｘ≧０の部分しかなかったりと、パラメータやｘ、ｙに制限がついているので、条件を正しく追いづらい。

②通過領域の問題は、計算量が多くなりがちなため、単独で問題が出されたり、出されたとしても問題の（２）や（３）など再度の方の「締め」として出題されることが多いが、今回は（１）で出題されているため、あまり時間をかけず（２）へ進めという意図を感じる

③実際に図形的に解くと、面倒な計算がほとんどなく一瞬で求められる。

というようなことを、２月２５日の当日にブログに書いたら、案の定、河合塾や駿台、東進など、軒並み図形的な解法をアップしてましたね。

私の手書きの解答では、①パラメータの解の配置　と、②ファクシミリ論法　の２つも合わせて載せておきました。
③包絡線は、理論的には使えるのだろうけど、この問題では使うべきではないと判断したので載せてません。

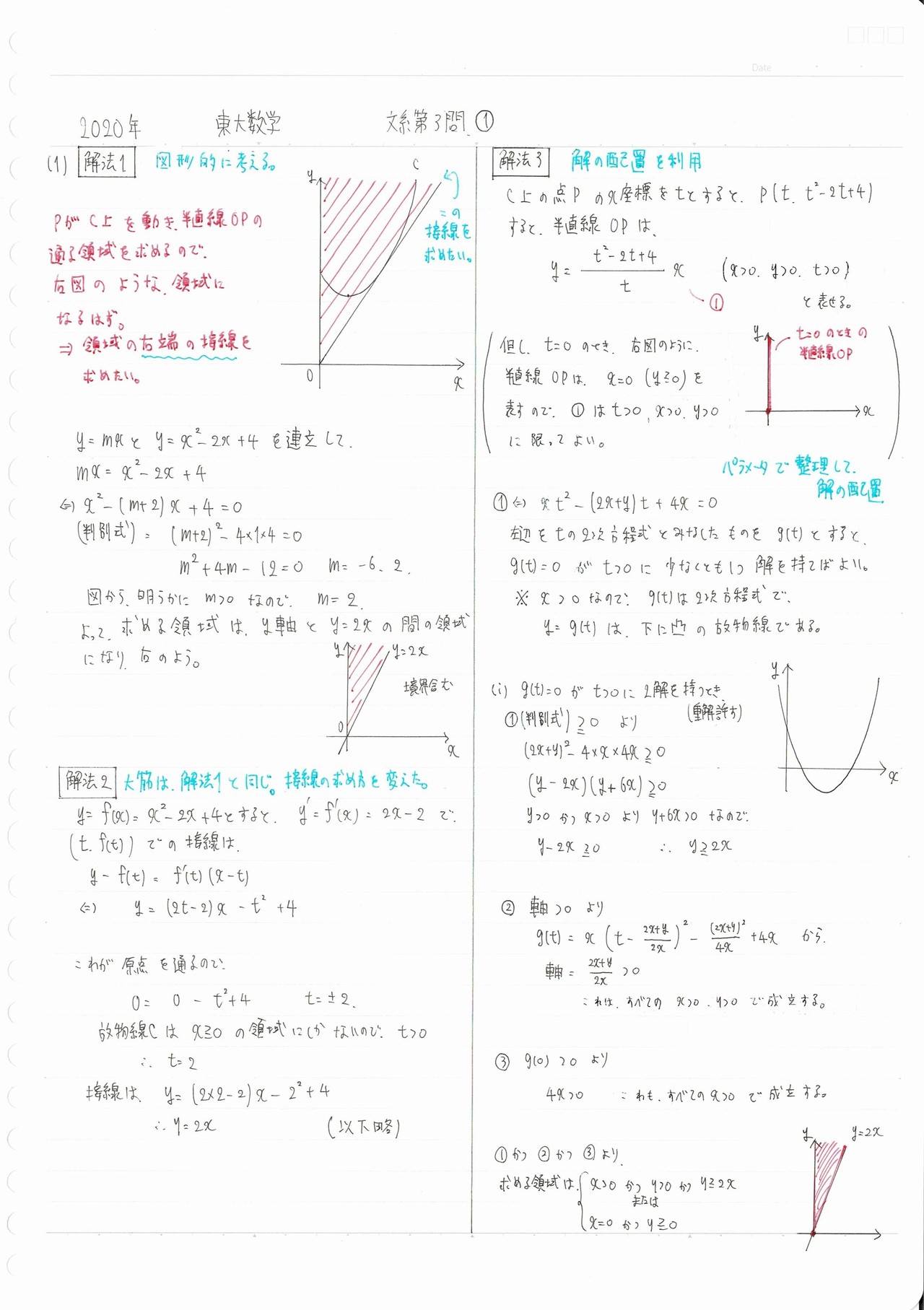
では、まず（１）の部分までご覧ください。

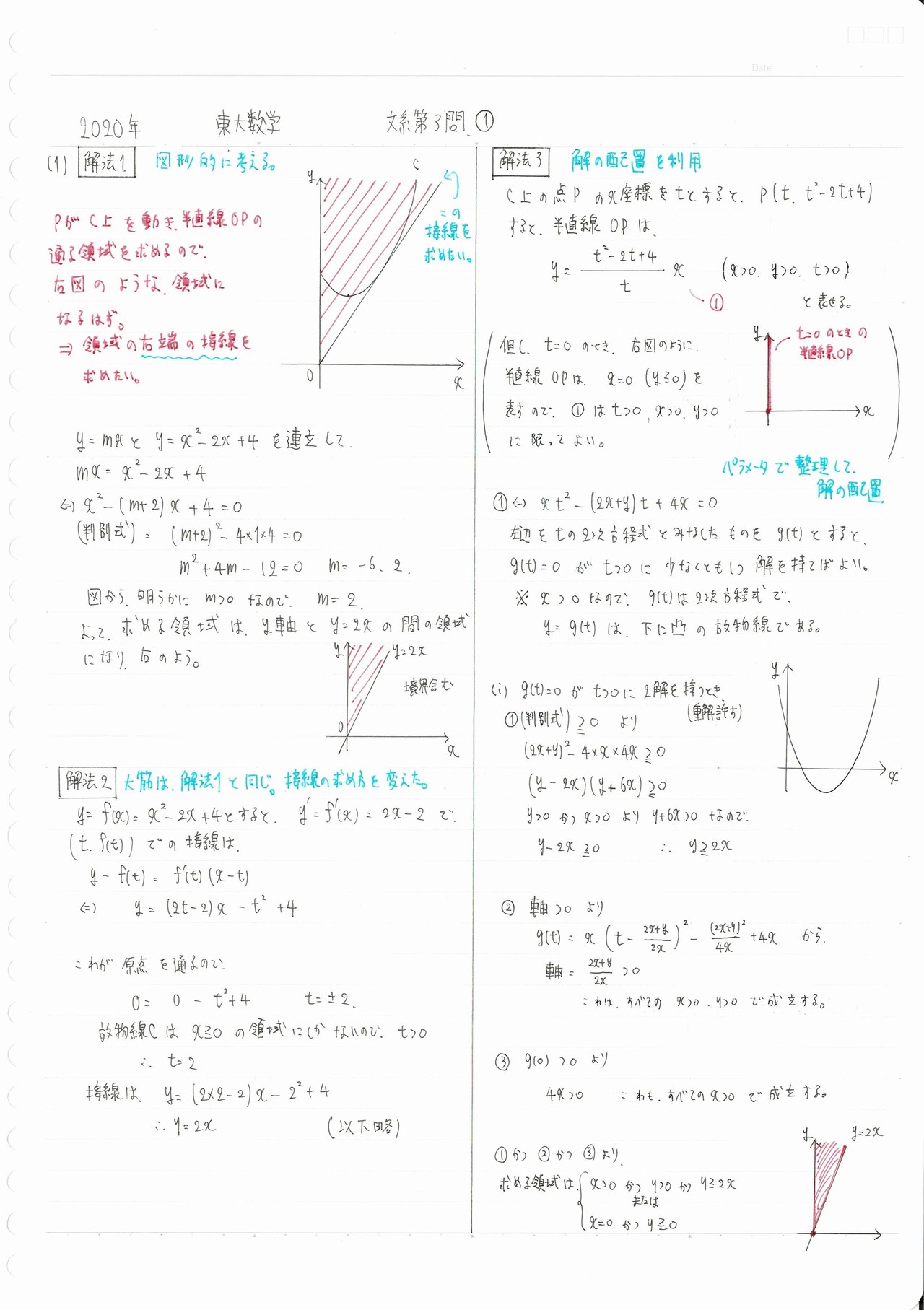
余談ですが、こういう風に一つの問題に対して、なるべくたくさんの別解の方針を検討して、どれが使えてどれが使えないかなどを考察するのが、一番数学力がつく方法です。
このブログは、この趣旨のもと、なるべく別解をたくさん載せようと思って記事をアップしていますので、やや更新が遅いのですが、その分皆さんの勉強になると思います。

（２）正三角形の条件をどうするか。

東大では、過去問でも直交座標上での正三角形の条件を出題しています。
正三角形だけでなく、二等辺三角形や、鋭角三角形に関する問題も出ていますから、当然大好きな問題と見てよいでしょう。
私は当然「お、出たな」と思って構えました。

参考
１９９８年第２問（鋭角三角形）
２００４年第１問（正三角形）
２０１１年第４問（二等辺三角形）
２０１６年第１問（鋭角三角形）

さて、この問題ですが、面白いのが正三角形の条件をあまり使わないんですね。
正三角形と言ったら、三辺が等しいとか、１角が６０度とか、色々な性質があります。色々な性質があるということは、解法がたくさん分岐するということですから、その分だけ考察時間がかかります。

しかし、この問題は、なんと角度が６０度ズレるということに気付けば解けてしまうという結論。
つまり、「正三角形が作れる条件」というのは、ややごまかされた条件で、実際は単純な角度６０度の問題なのです。
これに気付けると解ける人も多かったと思いますが、どれだけここまでこれたでしょうか。

座標と角度の問題はこう解け

最後
座標上で角度を扱う問題も、東大が大好きです。
さて、使えるツールとしては
①ベクトルの内積ｏｒ余弦定理
②ｔａｎの加法定理
③図形的考察
④ｔａｎ以外の加法定理
⑤（理系なら）複素数平面

の５つがありますが、上の２つが圧倒的に大事で、あとはあまり使いません。

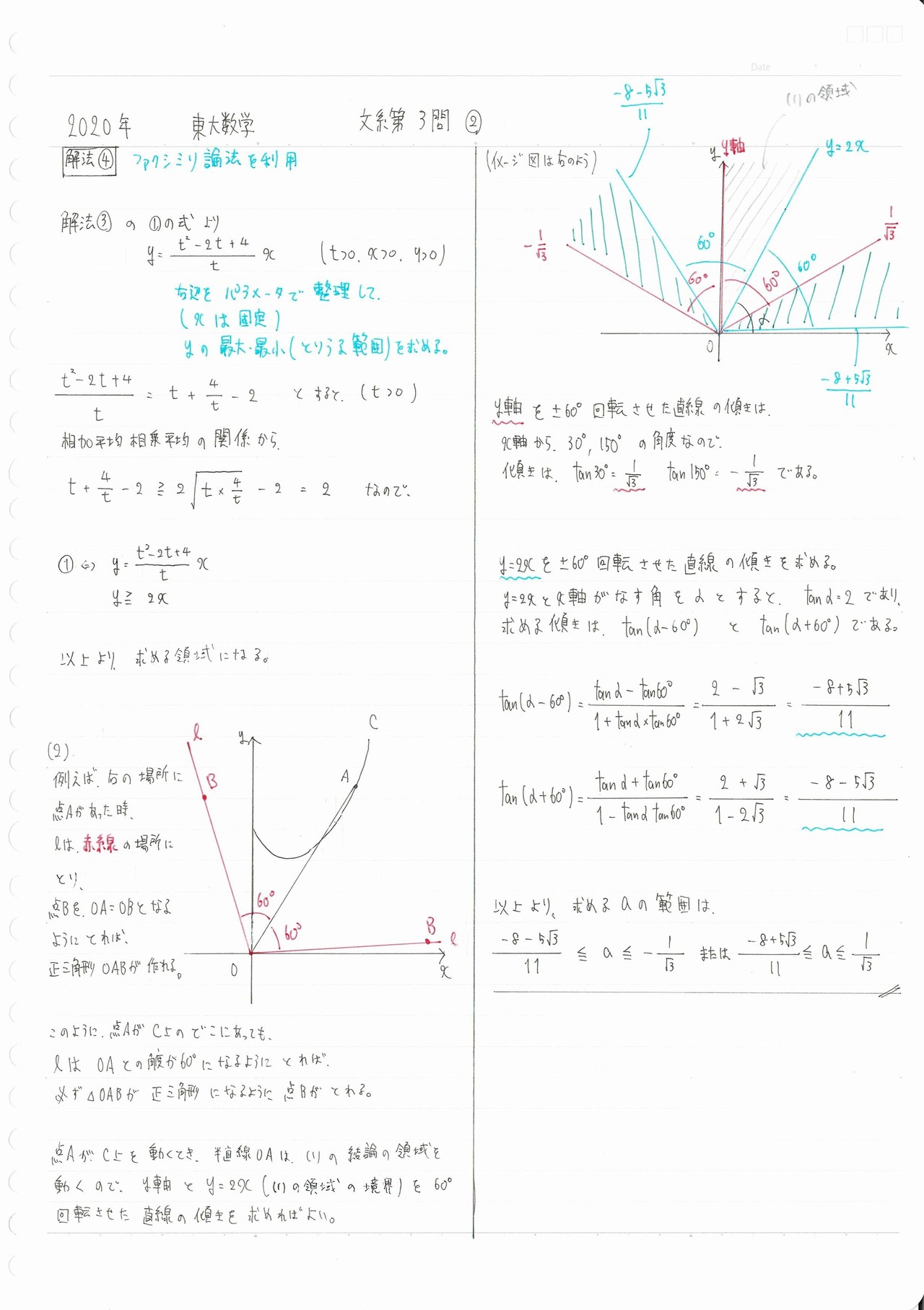
てことで、これを踏まえて、解答をご覧ください。

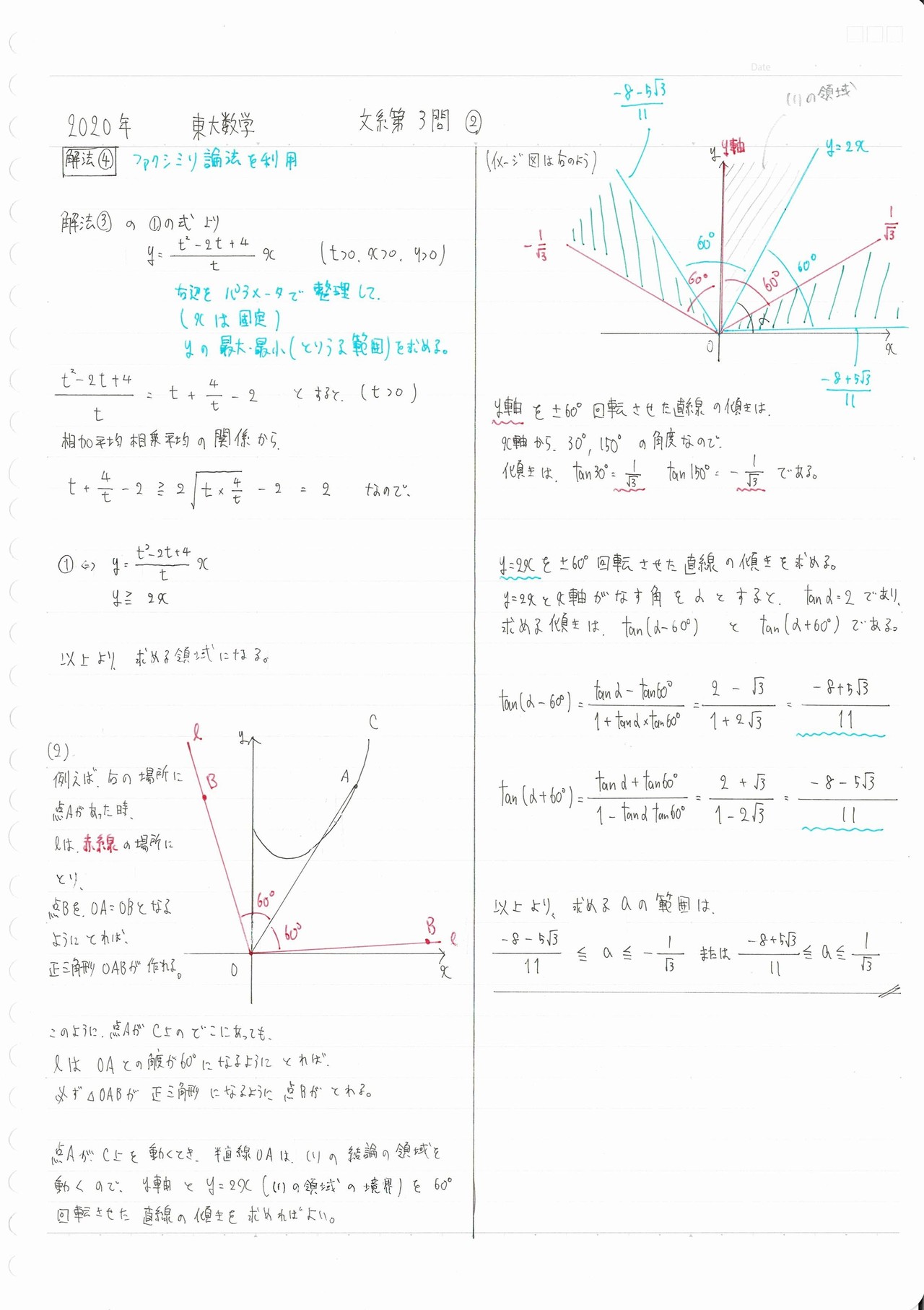
全体講評

今年の問題は、解き方が分かれば解けるけど、条件がひねられていて読み取りづらいセットでした。
これもその例にもれず。
座標と角度の問題は、頻出ですし、座標を三角形の問題も頻出ですから、よく過去問の分析をしておいてください！

敬天塾作成の解説

こちらのｐｄｆファイルは無料でダウンロードいただけます。
受験生の学習はもちろん、先生方の授業にお役に立てるのであれば、どうぞご自由にお使いください。
断りなしに授業時にコピペして生徒に配布するなども許可していますが、その際「敬天塾の答案である」ということを必ず明記していただくようお願いします。
ただし、無断で転売することは禁止しております。何卒ご了承ください。