数学９月④空間図形

こんにちは、スタッフAです。
今回は、空間図形です。
まず、空間図形と空間ベクトルは違うというアナウンスで授業が始まりました。
空間の分野は、ベクトル成分なしの場合は平面ベクトルと似ていて、ベクトル成分ありの場合は難解になるそうです。出題頻度も少なく、問題集にもあまり載っていません。
平面図形と空間図形には、共通する公式がいくつかありますが、成分と規定のベクトルにおいては公式が少し変わります。どう変わるかは、noteに文字で入力するのが難しいので、公式を見たときに、ああ、そう言えば「成分と規定ベクトルは少し変わる」って言ってたなあ、と思い出してください。

空間ベクトルのポイントはこの２つ。
①同一平面上の条件
②直行条件
どちらか、あるいは両方を使って解く問題がほとんどではないでしょうか。

メモ　図形において座標を導入するかどうかは、常に検討する。
メモ　解と係数の関係は、夕食のメニューを考える時一度炊飯器のご飯の量を確認するように常に検討する
メモ　最大最小問題なら、最初にグラフを検討する
メモ　ax+by+cz+d=0の平面に対する法線ベクトルのひとつ（a，ｂ，ｃ）
メモ　合同の定義　移動によってぴったり重なる図形
メモ　回転図形は難しい。座標と角度が出てきたら、tanθの加法定理かベクトルの内積など

最短距離を問われたら、線分です。

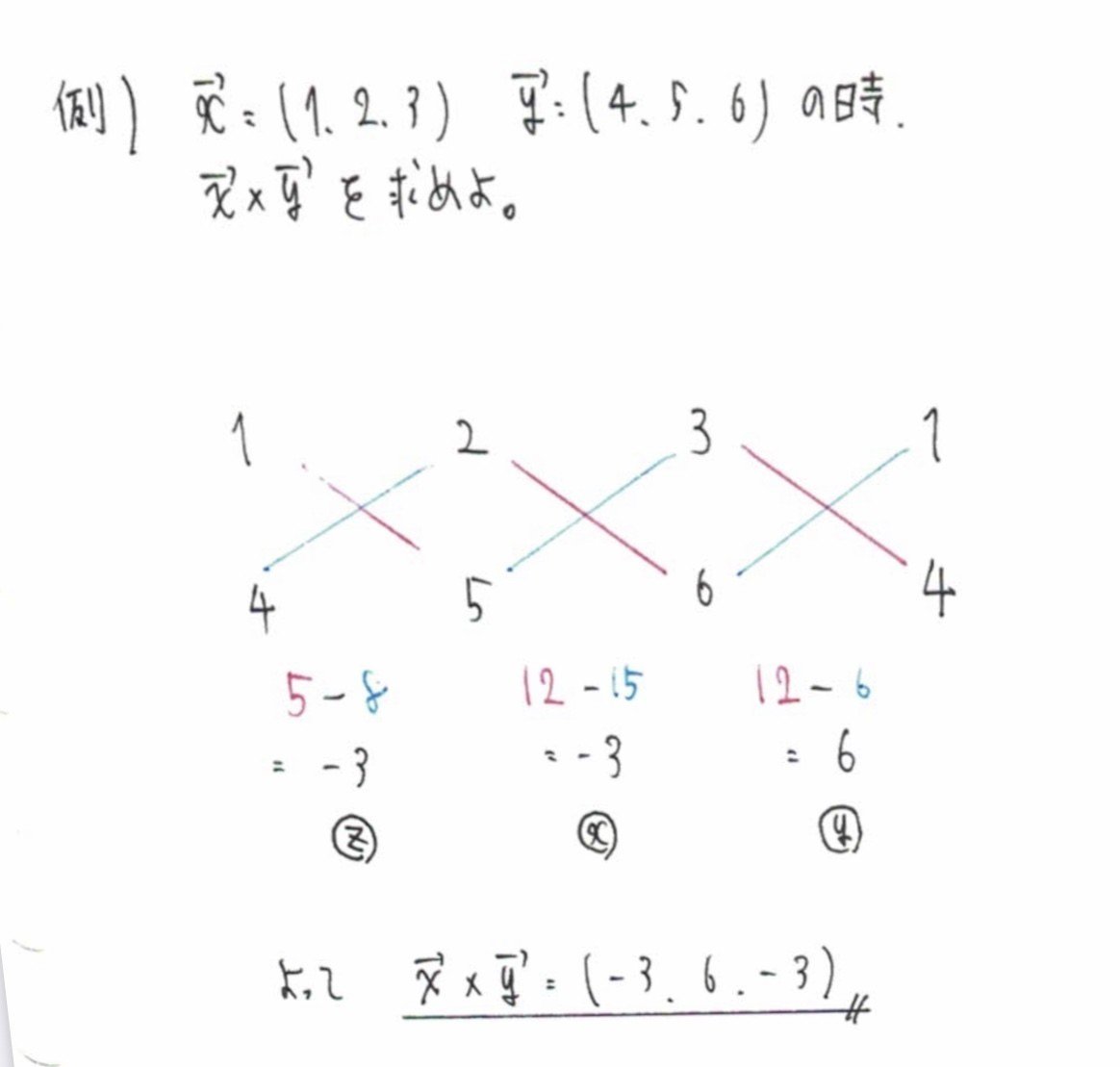
ベクトルの外積を紹介します。
外積を用いるメリットは、aベクトルにもbベクトルにも垂直なベクトルがすぐわかること。
詳細は、画像を御覧ください。

立体図形が出てきたら、対称性と切断を使うと思って良いです。

なぜかというと、体積→高さ→垂線→垂線の足の場所を特定する流れになるが、足の場所を特定するのはとても難しく、対象性のある図形の問題しか入試で出題されないからです。

メモ　立体図形の合同は習っていない。だから、ふわっと記述すれば許される。
例えば「対称性によって～～」
メモ　確率の対象性もふわっと記述して良い
メモ　面と面のなす角θを問われたら、交線となす角９０°の線２つのなす角のこと

正四面体の中点を結ぶと正八面体ができ、体積比は２：１。有名事実なので、覚えましょう。

お読みいただきありがとうございました！