東大は「守り」に入った！？

２０１５年以降、「整数の性質」という単元が数Aに組み込まれてから、東大の整数問題は変わったように思います。
旧課程には、整数を扱う単元がなかったのに整数の問題が出題されていたため、端的に言うと「なんでもあり」の問題が出されていた。しかし、新課程になり「整数の性質」が教科書に登場してから、教科書範囲を「守る」ように(笑)
個人的な印象なので、賛否あるでしょうが、私にはそう見えます。

特に、注目すべきは「余り」の扱いかた。
東大の整数の過去問を見ていると、あまりに注目した問題が多いように思います。
余りを扱う際に強力なツールが「合同式」。合同式が使えるのと、使えないのでは、天と地ほど解答能力が変わります。

そこで、今回も合同式を使って示していきましょう。

注この問題で登場する合同式において、法はすべて４です。

2021年　東大数学　文系第4問（整数の性質）

パッと見て難問。
整数の問題だということは分かるものの、類題を見たことはないでしょう。自分で考え、自分で方針を立てなければならず、文系受験者にとってはかなり厳しいでしょう。
文理共通問題でしたが、理系にとってもやや厳しめ。（結果論ですが）計算量も多く、設問数も多いため、正直言ってコスパの悪い問題です。

一つずつ見ていきましょう。

（１）これは簡単♪

まずは（１）。これは簡単です。

・KA＝LBは与えられた通り、立式しておく。
・「Kを４で割った余りが、Lを４で割った余りと等しい」は、合同式でK≡Lと素直に作る。
・求めたい結論、「Aを４で割った余りが、Bを４で割った余りと等しい」も合同式でA≡Bとしておく。

この３式をちょっといじるだけで解けます。

KA＝LBにおいて、等号は合同に変えて良いので、KA≡LBとする。
次に、K≡Lを代入して、KA≡KBとします。

この時点で、両辺からKを割れば、求めたいA≡Bが登場しますが、そんな雑なことはしてはいけません。合同式において割り算はご法度。そこで、もうひと手間加えます。

移項して、KAーKB≡０とし、因数分解を経て、K（AーB）≡０とします。

ここで、問題の設定である「KとLが正の奇数」が重要になります。
今回の合同式の法は全て４です。つまり、議論しているのは、全て４で割った余り。
対して、KとLは奇数なので、４（つまり法）とは互いに素です。

このように、Ｋと４が互いに素であることを確認すると、下の定理を利用して、（見かけ上）Ｋが両辺から割れます。

つまり、
K（AーB）≡０（ｍｏｄ４）　において、４とＫは互いに素なため、Ａ－Ｂ≡０　よって、Ａ≡Ｂ

のように変形でき、完成です。

では、手書きの解説もご覧ください。

合同式において、好き勝手に割り算をすることはできませんが、法と互いに素な数を因数に持つ場合、あたかも割り算をしたかのように計算ができるというわけです。

なお、「簡単だ」と申しましたが、実際の再現答案を見る限り、正答率はあまり高くありませんでした。
別に、合同式を使わなくても示せるのですが、受験生にとってはこのレベルでも解けないということです。整数を苦手にする受験生は多いですが、（１）が解けないようであると、（２）以降は積極的に解いたり理解したりせず、基礎的な問題集を徹底して解き、理解を進める方が良いでしょう。

（２）難問！題意をとらえるだけでも難しい

さて、今回一番の難問だったと思われる（２）へ行きましょう。

まず題意を読み取るのが難しい。
問題文を読んで、「あぁそんな奇数があるんだな。」くらいは読み取れるでしょうが、核心部分の「２の素因数の個数が同じ」まで読み取れるかというと、ややてこずるでしょう。

KA＝KBとなり、KとLが奇数です。当たり前ですが、奇数とは２で割り切れない数ですから、２の素因数は全てAとBに集約されていることになります。

たとえば、A＝２、B＝４としてみましょう。KA＝LBとなる奇数KLはありません。絶対に、２の素因数が割り切れずに残ってしまうからです。
一方、A＝6、B＝１０としてみたらどうでしょう。K＝５、L＝３としてみれば、等式が成立します。これは、AとBが持つ２の素因数が同数（１個ずつ）だからです。

つまり、題意は、「AとBにそれぞれ含まれる、２の素因数の数が等しいことを示せ。」です。これを乗り越えたら、次は計算です。

（２）計算も面倒。勇気リンリン

計算としては、AとBを階乗（ビックリマーク）で表現し、それぞれの２の倍数の部分を考えていく、という方針です。

そこで、早速、階乗で表現してみようとしますが、文系受験者の中では階乗の表現に慣れておらず、面食らってしまった方も多いでしょう。実際に、文系の再現答案ではほとんど全員が白紙提出でした。

Aを階乗で表現すると、

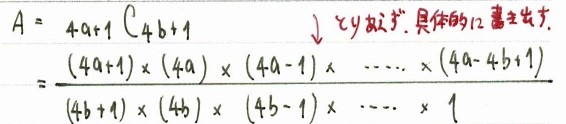
となり、ものすごい数の階乗の掛け算になります。
ここから、２で約分できるところを探していき、Bと比較する、というシンプルな方針ではあるのですが、手が止まってしまう人も多いでしょう。

結論を言うと、２の素因数が１個のところ（２×奇数のところ）と、４の倍数のところ（２の素因数が２つ以上のところ）に分割すると、ウマいこといきます。「２の素因数に注目しているから当然の発想だ」という声もあるでしょうが、普通は早速２で割り始めると思うので、私はこのタイミングで発想の難しさがあると思います。

私の手書きの解答では、このようにしていますが、

Aを階乗で表現した時点で、２で割りまくっても（順番が違うだけで）同じ結果が得られます。見づらいだけです。

この辺り、計算をゴリゴリ進められるか、それとも「面倒臭そうだな」と思って踏みとどまるか。結果を分かつものは勇気だと思います。

冷静であればあるほど、戦略的であればあるほど、面倒な計算に手を出すのが慎重になります。なぜならば、面倒な計算というのは、正解が得られるかわからない、ミスするかもしれないというリスクに加えて、時間がかかってしまうからです。

さてこの後ですが、上に手書きの画像のYとZの部分では、たくさん約分ができます。しかも「同数」で。
数えてみるとわかりますが、Yは分母と分子にｂ個ずつの４が含まれています。Ｚもｂ個ずつの２が含まれています。よって約分しまくった結果、４も２もなくなり、奇数だけが残ります。（なんか、偶数が粛正された感じ）

しかも、Ｙの部分に残ったのはＢそのもの。これで、ＡとＢが奇数の係数だけで等号でつながるのです。

以上をまとめ、解答です。

（３）まずは誘導の乗っかれ！

問題文を読むと、なんだか（１）（２）と同じような文言が並んでいます。
「ａ、ｂは（２）の通りとし、」とありますし、AやBの値も同じで、４で割った余りに関する話題も同じ。ということで、まずは状況を整理しましょう。

（２）で、KA＝LBとなることが示せました。
（１）では、KA＝LBで、かつ　K≡Lならば、A≡Bとなることがしめせています。
そして、（３）で示したいのは、A≡Bとなること。

これを整理すると、（３）で実質的に作業しなければならないのは、K≡Lとなることです。

（３）KとLを見比べよう！

では、具体的にKとLを見ていきましょう。

KとLは、（２）の最後に求めた、たくさんの掛け算です。
もともとは、（２）の途中で登場した、２×奇数の部分と４の倍数の部分、それぞれの分母と分子がルーツでした。
そこで、分割して、K＝K1×K2、L＝L1×L2としました。

この、たくさん掛け算された一つ一つについて、４で割った余りを考えます。
K1とL1は、４ａとか４ｂがたくさんありますが、どちらも４の倍数です。つまり、４ａ≡４ｂが成り立ちます。
すると、全ての括弧の中身が一致してしまうため、簡単に合同が示せました。

次に、K2とL2ですが、こちらは４ａや４ｂではなくて、２ａや２ｂが登場しています。
係数が２ではないので、合同が示せません。

そこで登場するのが、（３）の冒頭の「ａーｂが２で割り切れるとする」の部分です。
このままだと、２で割り切れるかどうかしかわからず使いづらい、そして今登場しているのは２ａや２ｂです。
そこで、２をかけてみましょう。
２ａー２ｂが４で割り切れることが分かります。つまり、２ａ≡２ｂ（ｍｏｄ４）です。

これで、K1とL1の時と同じように、K2とL2も一つずつすべて合同になることが示せました。

では、最後に全体をご覧ください。

（４）では、最後の仕上げだ！

さあ、集大成となる（４）。
問われているのはシンプル。しかし、もちろんそのまま２０２１の階乗や、３７の階乗を計算するわけではなく、（１）～（３）を利用します。

ここまでで証明されたことをまとめてみると、

・AとBに対して、必ずKA＝LBとなる奇数K、Lがある。さらに、ａ－ｂが２で割り切れる場合、Ｋ≡ＬかつＡ≡Ｂが成立する。

ということ。
これをさらに（４）で使う部分だけ取り出すと、

ａ－ｂが２で割り切れるならば、Ａ≡Ｂである。

となります。

さて、２０２１と３７に対し、ａやｂとなる数を探すと、５０５と９になります。５０５ー９が２で割り切れるため、
２０２１Ｃ３７　≡　５０５Ｃ９　が分かる。

５０５Ｃ９に対し、ａとｂになる数を探すと、１２６と２になり、１２６ー２が２で割り切れるため、
５０５Ｃ９　≡　１２６Ｃ２　が分かる。

このように、もともと２０２１や３７という大きな数だったのですが、（１）～（３）の結論を利用すると小さな数になりました。
あとは、実際に手計算で４で割ってみればＯＫ、という寸法です。

総括

文系にとってはかなり難問、理系にとってもそれなりに難問といえる問題でした。
発想力や計算力なども必要で、２５分で完答するのはかなり厳しいと言えるでしょう。

さて、解説では触れなかったことをいくつか付記しておきます。

一つ目は、４つの小問で構成されているため、一つ一つの配点が低くなるだろうということです。東大の配点は、第１～４問がそれぞれ２０点ずつだと言われています。（真偽は分かりません）
これを正しいと仮定すると、小問が多いほど一つの配点が小さくなり、コスパが悪い問題になります。

結果論ではありますが、この問題では（２）の計算量がまあまあ多いですし、全体として考察時間も多く必要でしょう。とすると、１問目に取り掛かるべき問題ではないと思われます。

二つ目に、（１）～（３）が解けなくても、（４）が解けます。（１）～（３）が証明問題なので、示すべき結論が書かれています。そこで、（４）だけ解くことが可能です。
もう少し細かいことを言うと、（１）が解けなくても（２）を解くことができます（難しくて解けないかもしれませんが）。

東京大学では、このように前の小問が解けなくても、次の小問が解けるという構成になっていることが、たびたびあります。今回のように、前の問題が誘導になっていても起こり得ますが、前後の問題が無関係ということもありますので、設問は最後まで目を通して、仮に（１）や（２）が解けなくても、（３）を解くようにすると点数が上がるかもしれません。

なお、前の問題を飛ばして次の問題を解いたときに、満点が与えられるかどうかは保証できませんが、一般的には一部または全部の点数が与えられることが多いだろうと思います。

敬天塾作成の解説

こちらのｐｄｆファイルは無料でダウンロードいただけます。
受験生の学習はもちろん、先生方の授業にお役に立てるのであれば、どうぞご自由にお使いください。
断りなしに授業時にコピペして生徒に配布するなども許可していますが、その際「敬天塾の答案である」ということを必ず明記していただくようお願いします。
ただし、無断で転売することは禁止しております。何卒ご了承ください。

【さらに深く学びたい方のために】

敬天塾では、さらに深く学びたい方、本格的に東大対策をしたい方のために、映像授業や、補足資料などをご購入いただけます。
ご興味頂いたかたは、以下のリンクからどうぞご利用下さい。

映像授業コース（旧オープン授業）【東大文系数学】