2023年東大文系数学（第2問）入試問題の解答（答案例）・解説
２０２３年東京大学 文系数学 第２問
（１）見事な練習問題の連続！
こちらも、第１問と同様、サクッと終わらせていきましょう！
まず、C上の点Pと直線ｌの距離ですから、点と直線の距離の公式を利用。すぐにｆ（ｔ）の正体が出ます。
この時大事なのが、ｆ（ｔ）の分子の絶対値は外れないこと。Ｃとｌのグラフを描いてみると分かりますが、Cとｌの上下関係は点Ｐの場所によって逆転します。
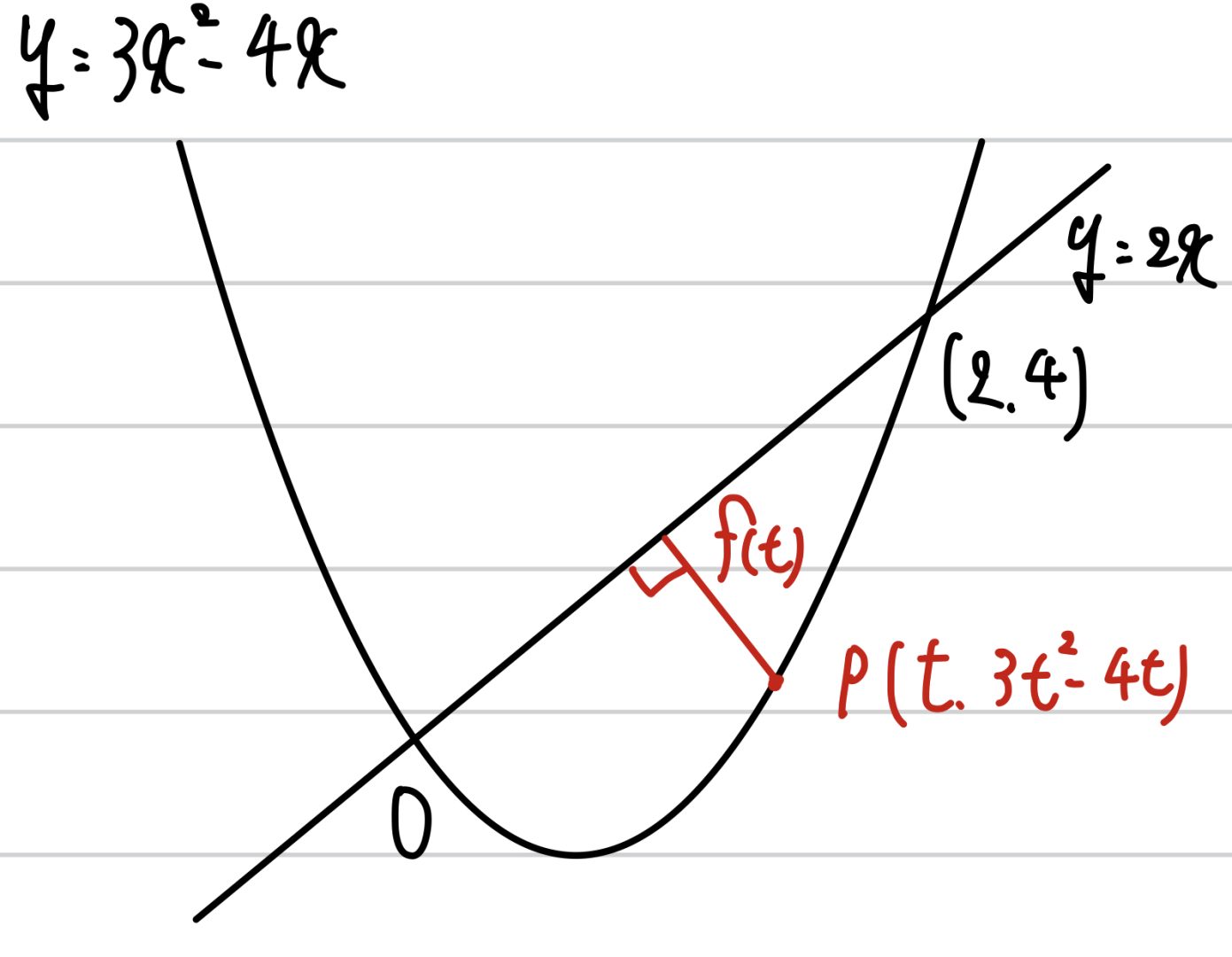
０と２の間なら直線ｌが上、０と２より外側にあると放物線Ｃが上です。このように上下が逆転するときには、絶対値は外せません。（どうしても外したければ、場合分けが必要になります。）
ここまでは、公式を使っただけの教科書例題レベル。
次に、この絶対値つきのｆ（ｔ）をインテグラルの中に入れて積分するのがｇ（ａ）です。
絶対値がついたグラフの定積分と言えば、これまた教科書の例題でよく見るタイプ。
ｆ（ｔ）は絶対値がついていますから、グラフで書くと横軸より下の部分がひっくり返って上になるわけですが、この時グラフの式が変更されます。
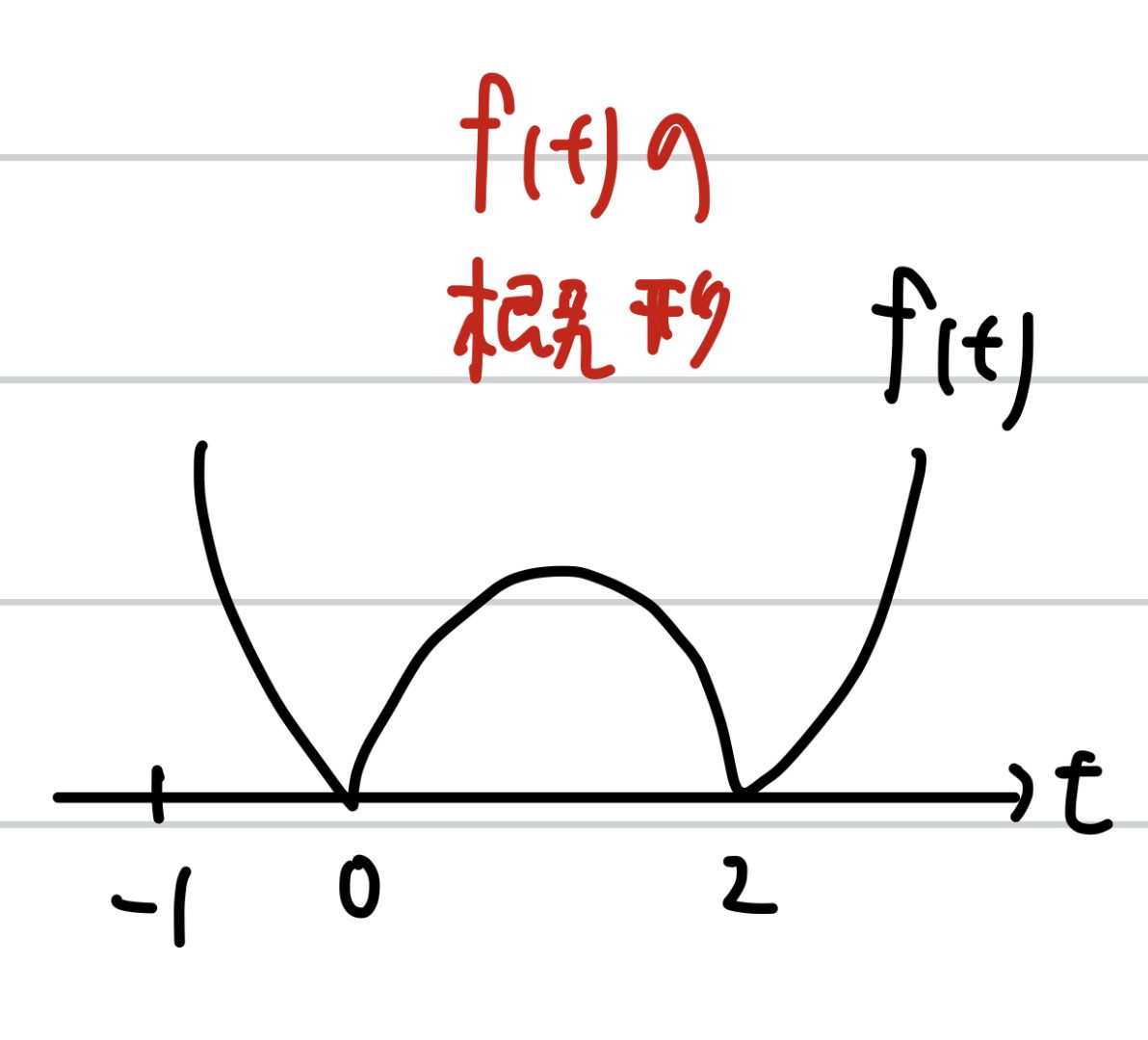
０と２の間は上に凸ですから、絶対値の中身をマイナスで外した場合で、０と２の外側は、下に凸ですから、プラスで外した場合の値です。
今回の積分区間は、ー１≦ｔ≦ａ。左端のー１は固定されているから良いとして、右端のａは動きます。つまり、ａがｆ（ｔ）の「折れ目」を超えるかどうかで場合分け。
よって、
（ⅰ）ー１≦ａ＜０の場合
（ⅱ）０≦ａ≦２の場合
という２通りの場合分けになります。
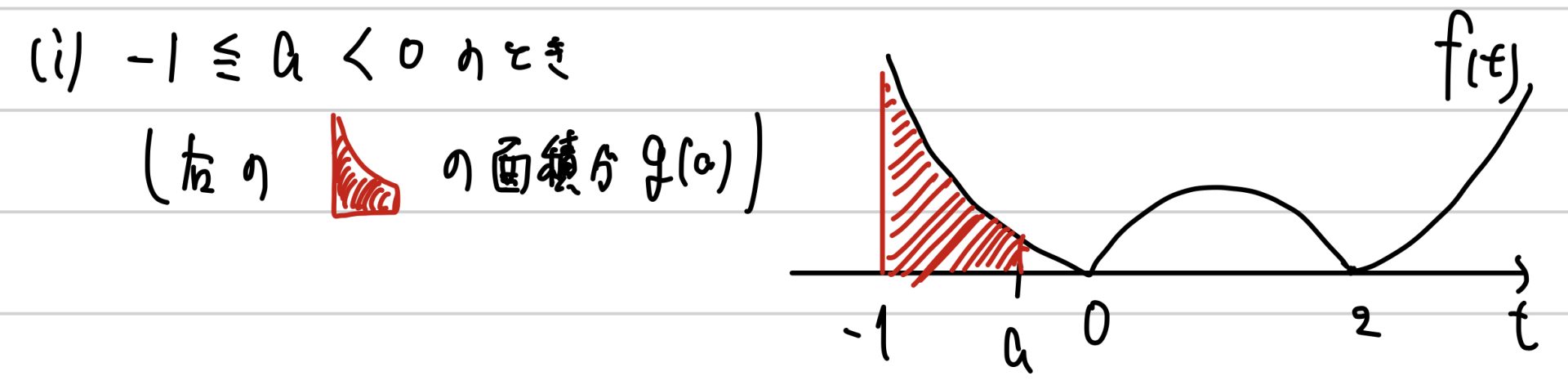
あとは、ｇ（ａ）を計算して終わりです。結局、教科書の例題を２問といているだけのような問題でした。
（２）これも教科書例題の連続
では、（２）へ行きましょう。
（２）では０≦ａ≦２と指定されているので、先ほどの（ⅰ）は無視。（ⅱ）の場合の計算結果のみを使います。
計算するのは、ｇ（ａ）ーｆ（ａ）ですが、（１）で登場したのはｆ（ｔ）。カッコの中身が違いますが、単にｔにａを代入するだけなので、困らないように。
さて、ｔにａを代入してみると、０≦ａ≦２ということで、絶対値が外れてしまいます。ｆの絶対値は０と２の間にあるか、外側にあるかで外れるという話でしたから、外してしまいましょう！
よって、ｇ（ａ）ーｆ（ａ）の値が絶対値ナシで明確になりました。
あとは、これの最大値、最小値を求めるだけ。
３次関数なので、微分して増減表を書いて、終わり！
計算ミスに気を付けて進めてください！
最後に、ａ＝２ー√２を代入するところがありますが、割り算を利用したり、次数を下げたりして工夫できるので、下の手書きのプリントで解き方を確認しておいてください！
2023(2)文数 解説
第１問につづき、これも取りやすい問題でした！
振り返ってみると、（１）も（２）も結局は基本の連続のみ。しかも教科書の例題レベルが連続して襲ってくるような問題でした。
計算ミスしやすいポイントがいくつかありましたが、ここでも「敵は計算ミス」の精神で慎重に進めてください！
【さらに深く学びたい方のために】
敬天塾では、さらに深く学びたい方、本格的に東大対策をしたい方のために、映像授業や、補足資料などをご購入いただけます。
ご興味頂いたかたは、以下のリンクからどうぞご利用下さい。
