科目全体

【敬天塾オリジナルレーダーチャート】

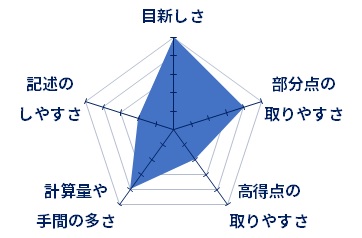
【各社の難易度比較】

※敬天塾以外の科目全体の分量、難易度は昨年比です。「同程度」「変化なし」は「昨年並」に表現を揃えております。
※敬天塾の科目全体の難易度は昨年比ではありません。
※設問別の難易度は全社、昨年比ではありません。
（以下、他の科目の各社難易度比較も同様です）

【科目全体の講評】

総合難易度　やや難

トピック①　高得点が取りづらい
第２問（２）や、第４問（２）（３）などは純粋に難しい問題。また第１問の円と３次関数が絡む問題や、第３問の通過領域の問題は新傾向と言ってよい問題です。
こういう問題が多いと、満点や高得点が取りづらくなります。
数学で高得点を取って逃げ切ろうという作戦だった受験生には不利な問題だったことでしょう。

トピック②　部分点が取りやすい
一方で、白紙答案にもなりづらい問題でした。
第１問は、満点は難しくても、連立するとかグラフを描こうとして微分するなど、数点の部分点なら簡単です。
第３問（１）は非常に簡単で、基本的な実数解の条件を使うだけでした。
第４問も（１）も合同式や余りの式を立てることは難しくなく、（４）は（２）や（３）を解かなくても答えることができる問題でした。

このように、去年（２０２０年）の問題と比べて、部分点が取りやすい問題だったと思います。

体感として、もともと数学が苦手で部分点狙いだった人にとっては、去年より簡単になったと感じただろうし、数学が得意で高得点を狙っていた人にとっては、かなり難しいと感じたセットだったのではないかと思います。

トピック③　パターン問題がなくなり、その場で考える問題ばかりになった。
「見た瞬間に方針が定まってあとは計算するだけ」のような問題は１問もなく、ゴチャゴチャ手を動かして、やっと概要が掴めてくる問題が増えた印象です。

もしかしたら、東大が典型パターン問題を封じに来ているのかも！？
それにしても、手を動かしていれば方針がちゃんと定まってくるレベル設定になっており、毎年ながら東大の先生方の問題作成能力は圧巻です。
また、一般の難易度判定では、純粋に問題の難しさばかりが論じられることが多いのですが、敬天塾ではどれくらい時間がかかるかも重視します。
今年の問題は、難易度そのものも高いと思いますが、方針を定めるのに時間がかかる上に、計算量もそこそこ多いということで、時間が圧迫されやすい問題も多かった印象です。

トピック④　設定が難しくなっている
第１問では、円と３次関数の共有点の個数の問題が出題されました。
一般的な問題集では、座標上で円と絡むのは、点か直線か円。たまに放物線。しかし今回は、３次関数との共有点ということで、他にあまり出題例のない問題でした。
また、第２問の場合の数の問題ですが、とても抽象度の高い問題で、事前に見たことがない設定だったと思います。
また、第３問では、東大ではお馴染みの通過領域の問題でしたが、これまで出題されてきた解法では通用しにくいタイプの問題でした。（詳しくは後述）
第４問でも、２つのコンビネーションの式を比較させ、偶数の数を数えさせるという、目新しい問題でした。

トピック⑤　だから、完答は難しい。部分点を稼ぐ勝負
知らない設定ということもありますが、もう一つ。
後半になると計算量が増えたり、場合分けが面倒になったり、論理が展開したりと、完答が難しい問題ばかりでした。
そのため、いかに部分点を稼ぐかが大事な印象。
もちろん、第３問の（１）みたいな、絶対取らなきゃいけない問題は、最重要なのは前提です。

トピック⑥　ある程度、最近の傾向を踏襲してきた
しかしながら、ある程度は予想通りの出題だったと言えます。

例えば、第２問に場合の数が出ましたが、敬天塾としては、「場合の数が出る（確率ではない）」と予想して、生徒向けに対策を促してきました。これは過去問を見ていれば自然な発想。
第３問の通過領域も、新傾向になるのは予想の範囲内で、今年最も力を入れて対策していました。
第４問の（１）の合同式も予想通りだし、整数の理論に絡む問題が出るだろうというのも、予想通りでした。

ということで、過去問は解くだけではなく、分析して傾向を掴むのも重要。
「とにかく過去問を解け」と絶叫する（される）場合は、もう一歩踏み込んで「東大側の心理」まで迫ってみると良いのでは？
「過去問＝解くもの」という発想だと、傾向の予想は出来ませんが、過去問を何度も並べて見返してみると、意外と予想できるものだな、というのが今年の問題の印象でした。

【2021年入試で注目したい問題はコレ！】

今年の第３問に注目してみましょう。
通過領域の問題ではありますが、ただの通過領域の問題ではありません。
東大受験の歴史を辿ると、いかに東大が手を変え品を変え、出題してきているかが分かります。

基本の解法
まず、基本を抑えましょう。
通過領域の問題の解法は、基本として抑えるべきものが３つあります。
１逆像法
２順像法
３包絡線の利用

但し、このうち１や２は問題集などで触れられていることもありますが、３の包絡線の利用に関してはややハイレベルで、使いこなせる人は少ないのが実情でしょう。

２０１４年第３問　包絡線を使わせる問題
ここを突いてきたのが、２０１４年第３問。リンク先で問題を確認してください。
２０１４年第３問の解説記事（https://exam-strategy.jp/archives/2004）

この問題は、「３包絡線の利用」が最適な解法だったのですが、それはともかく、１や２では非常に対応が面倒くさい問題でした。
そういう意味で、過去最高難易度の問題と言えるでしょう。パラメータが複数登場し、それぞれに範囲が設定されています。
このようなタイプの問題は非常に珍しく、対策が非常に困難でした。ちなみに、敬天塾では難易度判定を「難」を超えた「超難」に指定してました。

２０１７年第２問　ベクトルを使わせる問題
これに対し、２０１７年第２問では、上記の３つの方法のどれでもない、ベクトルの領域図示の問題が出題されます。
２０１７年第２問の解説記事（https://exam-strategy.jp/archives/851）
この問題も、それまでの傾向からあえて外してきた印象があります。

２０１８年第４問　ベクトルはベクトルでも「犬の散歩」
続いて２０１８年には、ベクトルの領域図示が連続して出題されます。
しかし、２０１７年が教科書でよく見かけるタイプの問題の応用だったのに対し、２０１８年では２つの図形が独立して動き、そのベクトルの和を求める問題。
僕は「犬の散歩」タイプの問題と呼んでいます。人が自由に動いた時に、リードに繋がれた犬が通過できる領域をもとめるようなイメ―ジです。
２０１８年第４問（https://exam-strategy.jp/archives/2641）

２０１９年第４問　ベクトルはベクトルでも、ベクトルの意味そのものを問う
そして２０１９年にもベクトルの領域図示の問題が登場。
但し、もちろん一筋縄ではいきません。今度は、領域を図示させるのがメインの出題意図ではなく、ベクトルそのものの理解を問うような問題にシフトチェンジしました。
２０１９年第４問（https://exam-strategy.jp/archives/2924）

２０２１年第３問　ベクトルから離れ、ダブルパラメータへ
さあ、ここまでの歴史を俯瞰した上で、今年の問題を再度見てください。
パラメータを含む関数が登場し、その関数が通過する領域を図示させる問題という意味では、２０１４年第３問まで先祖返りしました。
そう、先祖返りしているのです。あの「超難」指定していた２０１４年第３問と似ているパターンを持ってきました。
２０１４年第３問ほど複雑な設定になっていないのですが、同じパターンと言ってよいと思います。
こういう意味でも、様々考えさせられます。
過去問演習の大切さ、そして過去問を分析する大切さと、「ただ解けるようになっていればよいや」という甘い考えを封じる、東大の本気を感じる問題でした。

【2021年入試の傾向を踏まえると、今後の対策はどうする？】

① まず、過去問演習の重要性を強く認識しましょう

ここでいう「過去問演習」とは過去問を解けるようになるという（敢えて言いましょう）低レベルな話ではありません。
過去問をしっかり解いた上で、その解法を徹底的に習得し、問題ごとの別解の検討を徹底的に行い、同種の問題を比較した上で、さらに東大が次に攻めてくるポイントまで掴むということです。

ハイ、自分で言ってて、メチャクチャレベルの高いことだというのは認識しています。
ある意味、受験生への挑戦というより、指導者への挑戦だと言えるでしょう。

このレベルまで東大の問題を分析している先生がどれだけいるかわかりませんが、少なくとも（幸か不幸か）私は気付いてしまったので、早速次年度の指導カリキュラムに入れていこうと思います。

と、余談はさておき。
受験生の皆さんは、学校や予備校の授業を受けて復習するだけのような、受け身の姿勢から脱出する必要性を強く感じてほしいと思います。

② 特に注意すべき分野

これを踏まえた上で、特に注意すべき分野は、現時点でここだと思います。
・通過領域（過去問を完璧にした上で、応用パターンまで予測し対応しましょう。）
・場合の数（漸化式などではなく、面倒な場合分けや数え上げ、重複の削除を求める問題に注意）
・整数（偶奇、余り（合同式）、約数の個数、互いに素などのキーワードに注目。不定方程式の理論が重要）
・関数の基礎理論（グラフの描き方、交点の個数と方程式の解の個数の関係、実数解の条件など重要な基礎理論の理解）

この辺りに注目すると良いでしょう。