2021年東大文系数学(第三問)入試問題の研究
2021年東大文系数学第三問 実数解の条件と通過領域
講評
難易度
(1)易
(2)やや難
(1)はオマケの問題。
東大はほぼ毎年、0点にならないようにしれくれる簡単な問題を、こそっと残してくれている印象。
今年はこの(1)ですかね。(去年は第1問の条件a)
次は(2)これは中々難しいと思います。なぜかというと、一般的な通過領域のパターンでは見かけない設定になっているからです。
でも、これに気付くのは、通過領域について、ある程度の体系的な知識と解法の整理が必要です。
「とにかく解け」だとか「通過領域は全部このパターンで解け」みたいな指導をされている場合は、対応できなかったでしょう。
簡単に言うと、通過させたい関数に含まれているパラメータが1つなのが普通の問題で、この東大の問題は2つになっています。
パラメータには取りうる範囲が設定されるのですが、普通の問題は1つですから、ただの不等式1本で表現できます。しかし今回の東大の問題は2つなので、不等式1本では表現できず、領域になってしまうのです。
簡単に言えば、普通は習ってないパターンということ。
ということで、新しい設定の問題でした。
当日解いた所感

難易度 (1)易 (2)やや難~難
(1)はオマケの問題。
東大はほぼ毎年、0点にならないようにしれくれる簡単な問題を、こそっと残してくれている印象。
今年はこの(1)ですかね。(去年は第1問の条件a)
2つの放物線が交点を指定の場所に持つ条件ですから、連立して2次方程式にして、実数解の条件(解の配置)に持ち込めばOK。
今回は、ー1<x<0と0<x<1なので、f(ー1)>0とf(0)<0とf(1)>0と符号を設定すればOKですね。
次は(2)これは中々難しいと思います。なぜかというと、一般的な通過領域のパターンでは見かけない設定になっているからです。
でも、これに気付くのは、通過領域について、ある程度の体系的な知識と解法の整理が必要です。
通過領域の新パターンが登場!
普通、通過領域の問題の中で、最も簡単なパターンはこちら。
![]()
yとxの関係式に、aというパラメータが含まれていて、aの範囲が別で設定されています(今回は「aは実数全体」が範囲)
これが基本です。
しかし、この東大の問題に関していうと、放物線Cでは、yとxの式にaとbという2つのパラメータが含まれています。
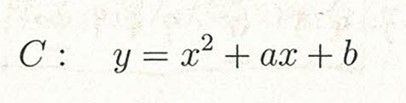
では、aとbの範囲はどこかというと、(1)で答えた領域です。(3本の不等式の重なる場所で、三角形になります)
言い換えれば、(1)は(2)の通過領域を求める際の、パラメータの定義域を求めるための問題だったということです。
まとめると、普通の通過領域の問題に対して、パラメータが1つ増えたパターンなのです。
ふつうの通過領域なら、この後、順像法、逆像法、包絡線の利用などの解法が考えられるのですが、パラメータが一つ増えた時にはどうするか。
普通は習ってこないパターンでしょう。
ということで、新しい設定の問題でした。
この問題の解法に関しても、もう少しちゃんと考察したら、体系的にまとめて何かしらの形で発表したいので少々おまちくださいませ。
ちなみに、通過領域の基本問題の解法などについてまとめた記事もありますので、良かったらどうぞ。
2014年 東大文系数学第3問 理系第6問① 通過領域の解法をノウハウにしよう!
2014年 東大文系数学第3問 理系第6問② すだれ法(ファクシミリ論法)と包絡線をマスターしよう
2014年 東大文系数学第3問③ 解の配置、すだれ法(ファクシミリ)、包絡線
2014年 理系第6問の解説④ 解の配置、ファクシミリ、包絡線

解説2021.jpg)

解説2021-300x161.jpg)