2021年東大文系数学（第3問）・理系（第1問）入試問題の解答（答案例）・解説（通過領域、逆像法、順像法など）

通過領域は毎年でる

【関連ページ】東大文系で頻出の通過領域の解法パターンをすべて紹介した決定版（逆像法・順像法・包絡線・線形計画法など）

今年も出ました、通過領域。
ここ最近の東大文系数学のブームです。

さて、問題です。東大文系では、どのくらい連続で出題されているでしょうか。
答えは２０１４年から毎年です。（２０１６年は除く）

こちらの画像をご覧ください。
最近の通過領域の問題1104

途中、ベクトルの領域図示の問題も混ざりましたが、様々な通過領域の問題が出ていることがわかるでしょう。

つまり、通過領域は２０２２年受験においても、攻略すべき最重要拠点だと言えます。

（上記の過去問の解説記事のリンクを張っておきます。）
２０２０年第３問
２０１９年第４問
２０１８年第４問
２０１８年第１問
２０１７年第２問
２０１５年第２問
２０１４年第３問その１
２０１４年第３問その２
２０１４年第３問その３
２０１４年第３問その４

この問題の手書きの解答の画像一覧を張っておきます。
ダウンロードや、ご自身の学習、先生方の授業での使用などは自由になさってください。（授業で使用する際は、敬天塾のものであると告知するようにしてください。）
無断での販売はご遠慮ください。

まずは、基本の３解法をマスターしよう！

通過領域マスターへの道は険しいです。
まず、数学ⅡBまでの内容を一通り把握することが前提。
次に、最大最小問題などのグラフを描く問題や、実数解条件（逆像法）が使いこなせるレベルでマスターする。
そして、基本の３解法を使い分けられるようになることです。

基本の３解法とは、①逆像法、②順像法、③包絡線の利用です。

この３解法、使いこなすのが難しいのは言わずもがな、意外とハードルが高いのが用語です。

例えば、包絡線は教科書には登場しない用語で、普通に高校に行って卒業しても習わないでしょう。
逆像法とは、いわゆる実数解条件とか、解の配置問題、逆手流と同じなのですが、別名がたくさんあるので、同一の解法だと理解するのさえハードルが高いです。
順像法も同様で、ファクシミリ論法、すだれ法などと呼ばれていることがあります。
また、予選決勝法（１文字固定）の考え方も使いますし、混乱の元になりそうです。

このように複雑なので、解法の名前を一致させるだけでも、一苦労。
そして、先生でさえも結構混乱していることが多く、そもそも通過領域の解法について体系的にまとまっている参考書や資料に出会うことが難しいというのも、受験生を苦しめている元凶のように思います。
だって、練習問題も入手しづらいし、入手したとしても、簡単順に並んでないわけですから。

とハードルだらけなので、なかなか大変なのです。

この記事では、包絡線以外の解法について、かなり詳しくまとめていますが、そもそも通過領域の３解法とはどういうものか、については解説していません。上でも紹介した２０１４年第３問の解説の際に、まあまあまとめたので、良かったらご覧ください。
２０１４年第３問その１
２０１４年第３問その２
２０１４年第３問その３
２０１４年第３問その４

※なお、私自身がこの記事を書いたときよりも、考察がかなり深まっているため、やや甘い部分やわかりづらい部分などあるかもしれませんが、どうぞご了承ください。

【関連ページ】東大文系で頻出の通過領域の解法パターンをすべて紹介した決定版（逆像法・順像法・包絡線・線形計画法など）

２０２１年　東大数学　文系第３問

では、この問題について書いていきましょう。

まずは（１）ですが、これは簡単な問題。２つの放物線が指定の範囲で共有点を持つ条件です。
素直に連立して、実数解の条件（解の配置）に持ち込めばＯＫ。
軽く流して、次へ行きましょう。

下の画像の左上の部分が（１）の解説です。

通過領域が登場！でも、普通じゃないぞ！

では、（２）へ。これが難問。通過領域の登場です。
何が難しいかというと、パラメータが２つ登場していることです。

通常は、通過領域の問題ではｘとｙに加えて、もう一つの文字（パラメータという。例えばｔなど）が混在した式が登場します。
つまり、「ｘとｙとｔの式」をいじるのが、通過領域の問題です。

これに対し、
①逆像法では「ｔが解として存在する条件をもとめることで、ｘとｙの領域を求める」
②順像法では「ｙ＝（ｔとｘの式）に持ち込み、右辺のｘを固定して、ｔを動かしながらｙの値域を求める」
③包絡線では「動いている曲線（直線かも）が、常に接しているような曲線があるかどうか探す。あったとしたら接点を求めて、接点を動かすことで、図形的に通過領域を求める。」
といったところでしょうか。
これが、大雑把にまとめた３解法です。

ちなみに、今回の問題は、放物線Cに登場するパラメータが１次ですね。（ａとｂ）
包絡線はパラメータが２次の時にしか、基本的には使いません。そのため、今回は包絡線は使いません。

パラメータが２文字の場合、どうするか？

では、今回の問題のようにパラメータが２文字に拡張したらどうするか。
別に、パラメータが２つになったからと言って解法が変わるわけではないので、原則として上の３つを検討すればよいです。

ただ、使い方が難しい。
なぜなら、理由の１つとして、パラメータを２つ使うとすると、解法が３つに分岐してしまうからです。

ｘとｙ、ａとｂ、ｓとｔなど２文字が登場したら、必ず考えるようにクセを付けてください。
①両方動かす
②片方を固定する
③もう片方を固定する
の３択が発生します。

先ほど、①逆像法と②順像法のどちらを使うかの選択があると言いましたが、
パラメータをどう扱うかで３択が発生するのです。

よって、６パターンの解法が生まれることになります。

※今回は、左上の解法をさらに２つに分けて、７つに分類しました。

この６つのパターンから最適なものを選んでいくことになります。

解法１～２：両方動かして逆像法

例えば、逆像法を使うとしましょう。
普通、逆像法（つまり解の配置問題）に持ち込んだ場合、多くが２次方程式の単元の一番最後に登場する問題に帰着します。
例えば、ｔ＞０という範囲が与えられていた場合なら、ｔ＞０に解を持つ条件を求めますから、判別式＞０と、軸＞０と・・・などと考えていくでしょう。

しかし、今回のようにパラメータが二つ登場したどうすればよいのか。つまり、パラメータが２つの場合の、解の配置問題とは、どういうものなのか？
結論を言うと、いわゆる線形計画法がそれにあたります。

線形計画法は軌跡と領域の最後の方に習いますが、おそらくほとんどの生徒が、
「領域を書いて、直線やら円やらが、領域とぶつかるように動かせばよい。」
など、解法を覚えていることと思います。
しかし、その根本的な意味はというと、おそらく何も考えてない笑。おそらく先生もあまり深く考えてないと思います。
私も最近気づきました。

そこを、よく考えてみると、いわゆる線形計画法の問題は、２文字の解の配置の問題なんですね。よって、これを使うことになります。
では、これを使った解法をご覧くださいませ。

解法１では傾きで場合分け、解法２では切片で場合分けをしています。

解法３～４：片方のパラメータを固定して、逆像法

さて、お次は、パラメータを片方固定して逆像法を使うパターンです。

この問題はパラメータがａとｂの２文字登場します。
「パラメータが多いなら、１つ減らしちゃえば良いじゃない。」
その通り。至極自然で合理的な発想です。

しかしながら、この解法は、おそらく多くの方が行き詰まると思います。
なぜなら、１文字固定は等式の場合に使うことは慣れているが、不等式に使うことに慣れていないからです。

今回の問題は、放物線C（ｘとｙとａとｂの式）が解を持つ条件を考えるのですが、
ａとｂが満たす条件はこの３不等式です。

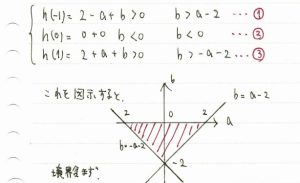
放物線Cの式に関しては、ａを固定でも、ｂを固定でも大したことはありません。
例えば、ａを固定したとしたら、「ｘとｙとａとｂの式」が「ｘとｙとｂの式」に変わるだけです。ａを数字と同じように扱えばすみません。

一方、不等式はどうでしょう。
もちろん、不等式が１つだけだったら簡単ですが、今回は３不等式があります。
ａを固定した場合、どのように扱えばよいのか、わかりますか？

おそらく、この技法はほとんどの方が習ってないので、できないということで当然です。

ということで、受験生にとっては、この時点で破綻した解法といってよいとおもいます。

一応、気になる方のために、ガイドラインだけでも作っておきました。

こちらをどうぞ。

ちょっとだけコメントをしておくと、
３本の連立不等式で表現された領域が、ａを固定、ｂを固定すると、それぞれ別の表現方法でも表現できます。
（この時、実は順像法の考え方を利用しています）。
つまり、３本の連立方程式で表現しても、画像に載っているような、ａ固定やｂ固定で作った式で表現しても、表している領域は同じなのです。
よって、（１）で求めた３本の不等式を利用せずに、解の配置を解くことになるのです。

解法５：ａとｂを動かして、順像法

では、次に順像法を利用する解法にいきます。
まず、ａとｂを両方動かす場合ですが、これは基本的に難しいです。

順像法では、ｙ＝（ｘとａとｂの式）と変形し、ｘを固定した上で、ｙの値域をパラメータを動かすことによって求めていきます。
この問題では、
ｙ＝ｘａ＋ｂ＋（定数項）という形になるのですが、ここで問題が発生します。
ａとｂをいくつにすると、最大（最小）になるのか不明。ということです。

ｂに注目すれば、ｂが大きければｙも大きくなり、ｂが小さくなればｙも小さくなるという関係性があります。
しかし、ｂを大きくすることによって、ｘａが小さくなってしまってはダメです。

実際に、ａとｂには従属関係といって、勝手にばらばらに動けない関係性があります。
証拠は（１）のこの図です。

①や②のようにａとｂの関係式があると、「勝手にｂだけ大きくする」ということができません。

ｙ＝（ａとｂの式）のような形を「２変数関数」というのですが、実は２変数関数の値域を求める問題は、大学受験に登場します。
しかも、ちゃんと数ⅡBまでの範囲で登場しているので、おそらくこれをお読みの皆さんも解いたことがあるはずです。

例えば、このような関数。

特に、一番したのパターンをご覧ください。
ａとｂの２次しきが登場し、それぞれを平方完成すると値が求められるという問題を解いたことがあると思います。
（通常、数Ⅰの２次関数の章末問題あたりで扱うのではないでしょうか。）

ただ、これ、よく考えると、ａやｂの片方を固定しているといえば、固定しているんですよね。
今回は、ａとｂを両方動かす場合の解法を考察しているんですが、結局は固定して考えてしまうことになります。

上の２つはそれぞれ、円の半径や傾きなどの図形的な特徴を表す式に帰着するから解けるというパターンです。
つまり、数式としてではなく、図形として解いています。

今回の問題で登場する、ｙ＝ｘａ＋ｂ＋（定数項）は、残念ながら何の図形もあらわさないと思うので、断念する解法でした。

解法６～７：ａとｂの片方を固定して、順像法

さて、最後に残った、解法６～７です。
これも、ａかｂを固定することになるので、解法３～４と同様に、不等式の領域に対して、ａやｂを固定しなければいけないので、この時点でおススメできない解法です。

ということで、とてもあっさりですが、一応途中まで解いたので、画像で確認してください。

まとめ

いやはや、学びの多い問題です。
パラメータの数による解法の分岐や、逆像法／順像法の解法の違いなども学べます。
本当は、順像法や逆像法の数学的な意味も説明した方が良いのでしょうが、キリがなくなってしまうので、これくらいにしましょう。

さて、この問題の解説を書くにあたり、インターネットを中心に様々な先生の解法や解説を参考にさせていただきました。
多くは解法１や解法２を説明したもので、解法の分岐などには触れていないものだったのですが、一つだけレベルの違う解説をされている先生がいらっしゃったので、大いに参考にさせていただきました。ありがとうございました。
（私の解説記事は、この動画をさらに丁寧に深ぼったという感じです。）
【伝説級の良問!?】2021年東大数学vs東大医学部（理系第１問、文系第３問）

２０２１年第１問（解説はここをクリック）と並べて、勉強すればかなりの数学力の向上になると思います。
また、２０２２年受験生は、他の入試問題と同じように扱ってはいけません。直前の過去問ほど重要です。
ぜひとも、思っている３倍くらいの重要度だと思って、しっかり復習してほしいと思います。

敬天塾作成の解説

こちらのｐｄｆファイルは無料でダウンロードいただけます。
受験生の学習はもちろん、先生方の授業にお役に立てるのであれば、どうぞご自由にお使いください。
断りなしに授業時にコピペして生徒に配布するなども許可していますが、その際「敬天塾の答案である」ということを必ず明記していただくようお願いします。
ただし、無断で転売することは禁止しております。何卒ご了承ください。

【さらに深く学びたい方のために】

敬天塾では、さらに深く学びたい方、本格的に東大対策をしたい方のために、映像授業や、補足資料などをご購入いただけます。
ご興味頂いたかたは、以下のリンクからどうぞご利用下さい。

【関連ページ】東大文系で頻出の通過領域の解法パターンをすべて紹介した決定版（逆像法・順像法・包絡線・線形計画法など）

映像授業【東大文系数学】