東大文系数学においての、場合の数・確率の歴史ダイジェスト

東大文系では、2017年までほぼ毎年、確率の問題が出題されていました。
2018年では、場合の数・確率からの出題はなく、2019年以降は場合の数からのみ出題されています。

つまり、ここ数年で、明らかに確率から場合の数に、出題傾向がシフトチェンジしたと分析することができます。
（念のため付記しておきますが、だからといって次の入試で場合の数が出題されると予想しているわけではありません。）

また、確率が出題されていた２０１７年までを俯瞰すると、
２０１５年まではいわゆる「確率漸化式」の問題がほぼ毎年出題されていましたが、
２０１６年と２０１７年では、「確率漸化式」ではない、確率が出題されました。

以上をまとめると、以下のようにまとめることができます。

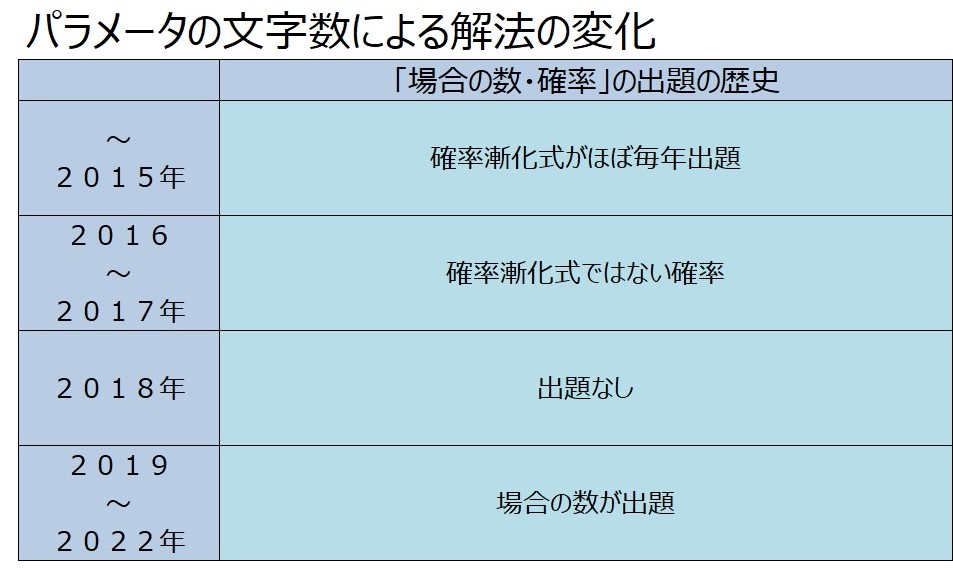
近年の場合の数・確率の傾向

では、確率漸化式以降の問題に、何かしらの共通点や傾向があるのかというと、（大雑把に言って）あります。

・場合分けが出る
・（鮮やかに解くというより）愚直に数え上げる問題が出る
・難易度はだんだん上がっている

といった感じでしょうか。
詳しく知りたい方は、以下のリンク先をご覧くださいませ。
２０１６年第２問の解説記事
２０１７年第３問の解説記事
２０１９年第３問の解説記事
２０２０年第２問の解説記事

要するに、「見た瞬間パッと思いついて解く」というような問題ではなく、知らない設定の問題が登場して丁寧に読み込み手を動かしながらカラクリを解き明かす問題が出るということです。
ある意味、数学の王道といえるかもしれませんが、受験生にとっての負担は大きい。
２５分平均で問題を解き、答案を作成するとなると、時間は非常に短く感じるでしょう。

難易度も、ドンドン高くなってきているため、対策が難しく、得点も取りづらくなっていると思います。

では、以上を踏まえて、２０２１年第２問を見ていきましょう。

2021年　東大数学　文系第２問　解説（場合の数）

やはり、知らない設定の問題が登場しています。（まあ、場合の数・確率で知っている設定が出ること自体が少ないですが）
仕方ないので、手探りで法則を探っていくしかありません。

やることとしては、一般的な文字を具体的で小さい数に固定して考える、というのが定石。
今回の問題でいうと、Nが一般化している文字なので、Nに具体的な値を代入します。問題文からN≧５とあるので、N＝５を代入して考えてみましょう。

「１は必ず一番左におく」という条件を忘れやすいので、気を付けましょう。
（実際、再現答案にて忘れている答案が散見されました。）

書いてみると、５通りあります。
５通りあること自体にも意味がありますが、ここでは
・なぜ５通りになるのか
・５通りの中でグループ分けできるか（のちの場合分けの方法のヒントになる）
・N＝６にするとして、N＝５の場合が利用できるか
などが大切な視点でしょう。
つまり、「一般化するためのヒントを探るためにN=５の場合を検討しているのだ」というのを忘れずにいることです。

さて、５通りを書くと、
（３，５，７，９）
（３，５，７，１０）
（３，５，８，１０）
（３，６，８，１０）
（４，６，８，１０）
となります。
※１は必ず一番左で、左から２番目は必ず２になるため、簡単のため省略しています。

すると、この５つは、「奇数から偶数に切り替わるポイント」によって、５通りに分かれていることが分かります。
例えば、（３，５，８，１０）の組は、５から８になるところに「奇数から偶数に切り替わるポイント」が存在しています。

（３，５，７，９）は、全て奇数なわけですが、これは「奇数から偶数に切り替わるポイント」がなかったと捉えてもよいし、右に追いやられてしまったととらえてもよいでしょう。

このように、左の方は奇数が並んでいて、右の方は偶数が並ぶ、という法則に気づけば、あとはこれを、一般化して答案に書くのが、（１）の問題です。
ただ、これを記述するのがやや難しいでしょう。
論理的に正しく、正確な答えが導けているならば、答案として「アリ」でしょうが、それでもなかなか難しいかもしれません。
さっきから登場している「奇数から偶数に切り替わるポイント」を「ｋ番目の奇数」か何かでおいて、ｋを動かすというのが一般的な思考のように思いますが、別解も含めて手書きで示しておいたので、どうぞご覧ください。

（２）　さあ、どう攻める！？

さて本丸の（２）。
（１）が２連続する場所を考えるのに対して、（２）ではＮ－２連続する部分を考えます。

冒頭にも書いた通り、ここ最近の東大では鮮やかな解法で解かせるわけではなく、愚直に場合分けを求めてきます。
よくテクニックとして「”少なくとも”があったら余事象を使え」とありますが、余事象を使う路線を検討しても、あまりスッキリいかない。
ここは、過去問の傾向にも習って、面倒でも正面から場合分けをするのが妥当な解法だと考えましょう。

ここで注意するのが、「Ｎ－２連続する部分を含む」というのは、「ちょうど」ではないということ。Ｎ－１連続やＮ連続でも、条件を満たします。これをヒントに「ちょうど」連続する数で場合分けをするのが、シンプルで発想しやすいでしょうか。

（ⅰ）ちょうどＮ連続する
（ⅱ）ちょうどＮ－１連続する
（ⅲ）ちょうどＮ－２連続する

の３つに場合分けをすれば、排反に分けられます。

この方針で丁寧に解いたのが以下の解法１です。
（かなり、補足の図などを書いて、場合の数を数えやすくしてあると思います。）

（２）別解法：連続する部分の最小値で場合分け

別解法も見つけたので、書きました。
こちらは、「連続する部分の最小値」で場合分けするというもの。「ちょうど」ではないため、連続する部分は「Ｎ－２連続以上している」としています。

ただし、このような場合分けをすることは稀なので、受験生が試験会場で思いつけるかどうかというと、怪しいと思います。
解法を盗むのは当然としても、１手目に考える解法ではないと思いますので、あくまで選択肢の１つとして味わってください。

まとめ：難問。（１）を確実に取ろう

ここ数年の東大文系では、場合の数・確率の問題が難しく、高得点を取るのが非常に厳しいと思います。
再現答案なども見ましたが、良くて（１）が得点できている答案ばかりで、０～５点ばかりでした。

確かに、過去問を解いていると、愚直に場合分けする問題が多いというのは気づけますが、過度な緊張状態にある試験会場で、正解にたどり着く場合分けの方針を思いつき、数えミスと計算ミスをせずに正解するというのは、非常に厳しいと思います。

「どこまで攻めるか」という見極めが大事であり、この問題に時間をたくさん投下するならば、相当な覚悟をするべきでしょう。

一方で、練習問題としては非常に良い問題といえます。
場合分けの方針の検討や丁寧な数え上げの訓練としては良問だと思います。非受験学年の生徒さんは、解いたうえで時間をかけて分析して、力を蓄えると良いと思います。

敬天塾作成の解説

こちらのｐｄｆファイルは無料でダウンロードいただけます。
受験生の学習はもちろん、先生方の授業にお役に立てるのであれば、どうぞご自由にお使いください。
断りなしに授業時にコピペして生徒に配布するなども許可していますが、その際「敬天塾の答案である」ということを必ず明記していただくようお願いします。
ただし、無断で転売することは禁止しております。何卒ご了承ください。

【さらに深く学びたい方のために】

敬天塾では、さらに深く学びたい方、本格的に東大対策をしたい方のために、映像授業や、補足資料などをご購入いただけます。
ご興味頂いたかたは、以下のリンクからどうぞご利用下さい。

映像授業コース（旧オープン授業）【東大文系数学】